链表及模板

1.注意事项

    这里讲述的都是用数组来模拟链表。为什么要用数组来模拟链表呢？原因如下：
        1.  数组相比于之前所学的动态创建链表，效率更高。
        2.  用数组实现更加简洁，操作简单。
    因此，这里采用数组来模拟链表，模拟单链表和双链表两种。

2.单链表和双链表的应用

    1.  单链表主要用来表示邻接表，邻接表实际上就是n个单链表组成，邻接表主要用来存储树和图。
    2.  双链表主要用来优化某些问题。

3. 单链表定义

4. 数组实现单链表

    在这里，我们用数组e来表示单链表中每个节点的值，而用数组ne来表示单链表中每个节点的next指针,head代表头节点的指针，表示头节点的下标。那么如何将节点与这两个数组关联起来呢，我们用下标就可以了。例：下标0表示单链表中编号为0的节点，e[0]代表单链表中编号为0的节点的值，而ne[0]代表单链表中编号为0的节点的next指针。对于剩余节点也是如此。需要注意的是，我们用值-1来表示单链表的结尾。idx代表接下来使用的节点编号是多少。
    注意：在这里下标只用来实现单链表，并不做查找节点的用途，换句话说：下标为5的节点并不一定是单链表中第6个节点，想要查找单链表中第6个节点的话，需要从头指针开始，依次通过next指针来寻找，而不是通过下标。非常重要！
    当然上述的注意并不适用于所有情况，需要具体问题具体分析，比如下述的例题就是需要通过下标来进行单链表操作的。

    关于单链表的初始化问题：
        单链表在初始的时候，head指针应指向为空，单链表中没有任何节点。因此：head = -1，idx = 0;

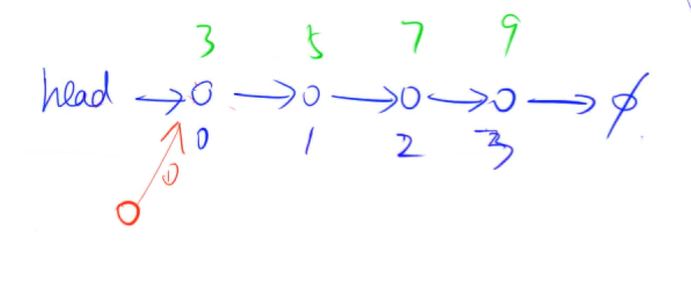
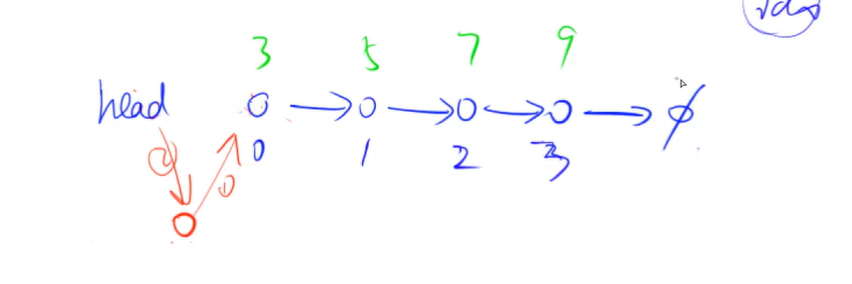
    关于单链表的插入操作：
        注意，我们这里的插入操作特指将节点插入到头指针的位置。（插入之后新的节点成为了第一个节点）具体步骤请看上图：
        操作如下：
            1. e[idx] = value;
            2. ne[idx] = head;
            3. head = idx++;

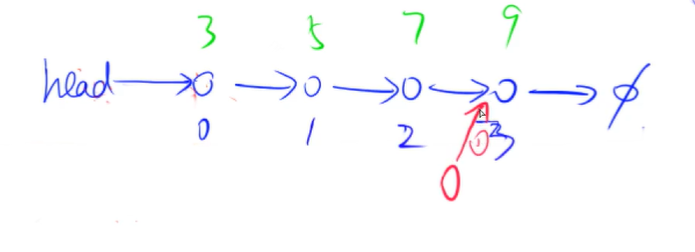
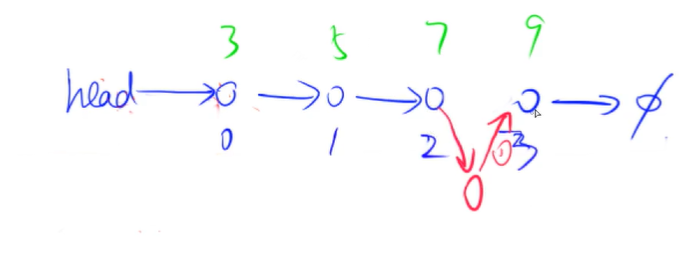
    关于单链表的插入操作1：
        注意，我们这里的插入操作特指将节点插入到单链表中第i个节点（不是下标为i）的后面。具体步骤请看上图：
        操作如下：
            假设我们已经遍历到了第i-1个节点，获得了第i个节点的下标k。(ne[i-1])
            e[idx] = value;
            ne[idx] = ne[k];
            ne[k] = idx++;

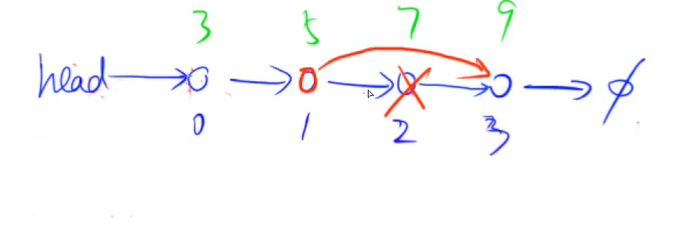
    关于单链表的删除操作：
        注意：我们这里的删除操作特指将单链表中第i个节点的后面的节点删掉。具体步骤请看上图：
         操作如下：
            假设我们已经遍历到了第i-1个节点，获得了第i个节点的下标k。(ne[i-1])
            ne[k] = ne[ne[k]];

5. 单链表模板

// head存储链表头，e[]存储节点的值，ne[]存储节点的next指针，idx表示当前用到了哪个节点
int head, e[N], ne[N], idx;

// 初始化
void init()
{
    head = -1;
    idx = 0;
}

// 在链表头插入一个数a
void insert(int a)
{
    e[idx] = a, ne[idx] = head, head = idx ++ ;
}

// 将头结点删除，需要保证头结点存在
void remove()
{
    head = ne[head];
}

6. 例题

https://www.acwing.com/problem/content/828/

    例题中的第k个数是按照时间顺序来的，即第一个插入的数，下标为0，第二个插入的数，下标为1，以此类推。
    而本博客中，k所讲述的是单链表中的第k个数，如果是这样的话，就不能通过下标来进行索引。毕竟，按照这种思路的话，单链表中的第k个数，下标未必是k-1。
    这里按照时间顺序，即下标来进行操作单链表。

#include <iostream>
#include <cstdio>

using namespace std;

int e[100010];
int ne[100010];
int idx;
int head;

void init(){
    head = -1;
    idx = 0;    
}

void deleteNode(int k){
    ne[k] = ne[ne[k]];
}

void insert(int k,int x){
    e[idx] = x;
    ne[idx] = ne[k];
    ne[k] = idx++;
}

int main(){
    char op[2];
    int m,number;
    scanf("%d",&m);
    init();
    while(m--){
        scanf("%s",op);
        if(op[0] == 'H'){
            scanf("%d",&number);
            e[idx] = number;
            ne[idx] = head;
            head = idx++;
        }else if(op[0] == 'D'){
            scanf("%d",&number);
            if(number == 0){
                head = ne[head];
            }
            deleteNode(number-1);
        }else{
            int x;
            scanf("%d %d",&number,&x);
            insert(number-1,x);
        }
    }
    int i;
    for(i=head;ne[i] != -1;i = ne[i]){
        printf("%d ",e[i]);
    }
    printf("%d",e[i]);
    return 0;
}

7. 双链表的定义

    双链表的定义只是在单链表的基础上，对节点添加了前驱指针而已。

8. 数组实现双链表

    在这里，我们用数组e来表示某个编号的节点值。
    我们用数组l来表示某个编号的节点的前驱指针。
    我们用数组r来表示某个编号的节点的后继指针。

    我们如何进行双链表的初始化呢？
        1. 在这里，我们不打算采用head指针的形式。而是用下标为0的节点代表双链表中最左侧的节点，下标为1的节点代表双链表中最右侧的节点。如果要这么进行初始化的话，idx从2开始。
        2. 在进行初始化的时候，我们打算让下标为0的节点的后继指针指向下标为1的节点。让下标为1的节点的前驱指针指向下标为0的节点。
        3. r[0] = 1;
           l[1] = 0;
           idx = 2;

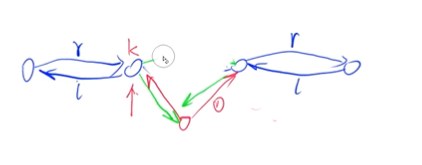
    我们如何实现双链表的插入操作？
        假设，我们要从下标为k节点的右侧插入一个新节点x，此时应该怎么做？
        1.  先赋值。
        2.  见上图。
        3.  具体操作如下：
            e[idx] = x;
            r[idx] = r[k];
            l[idx] = k;
            l[r[k]] = idx;
            r[k] = idx++;
        那么，如果我们要从下标为k的节点的左侧插入一个新节点x，此时应该怎么做？
        实际上，上述的操作等价于在l[k]的右侧插入一个新节点x，我们可以复用上述的操作即可。
        即，insert(l[k],x);
    因此，根据上述逻辑，双链表的插入操作只需实现一个即可。

    我们如何实现双链表的删除操作？
        假设，我们要删除下标为k的节点，此时应该怎么做？见上图即可。
        步骤如下：
            1. r[l[k]] = r[k];
            2. l[r[k]] = l[k];

9. 双链表模板

// e[]表示节点的值，l[]表示节点的左指针，r[]表示节点的右指针，idx表示当前用到了哪个节点
int e[N], l[N], r[N], idx;

// 初始化
void init()
{
    //0是左端点，1是右端点
    r[0] = 1, l[1] = 0;
    idx = 2;
}

// 在节点a的右边插入一个数x
void insert(int a, int x)
{
    e[idx] = x;
    l[idx] = a, r[idx] = r[a];
    l[r[a]] = idx, r[a] = idx ++ ;
}

// 删除节点a
void remove(int a)
{
    l[r[a]] = l[a];
    r[l[a]] = r[a];
}

10.例题

https://www.acwing.com/problem/content/description/829/

#include <iostream>
#include <cstdio>

using namespace std;

int e[100010];
int l[100010];
int r[100010];
int idx;

void init(){
    r[0] = 1;
    l[1] = 0;
    idx = 2;
}

void insert(int k,int x){
    e[idx] = x;
    r[idx] = r[k];
    l[idx] = k;
    l[r[k]] = idx;
    r[k] = idx++;
}

void deleteNode(int k){
    r[l[k]] = r[k];
    l[r[k]] = l[k];
}

//这道题的idx从2开始，因此要注意一下题目中第k个数与idx的对应关系。
int main(){
    int m,x;
    string op;
    scanf("%d",&m);
    init();
    while(m--){
        
        cin >> op;
        if(op[0] == 'L'){
            scanf("%d",&x);            
            insert(0,x);
        }else if(op[0] == 'R'){
            scanf("%d",&x);
            insert(l[1],x);
        }else if(op[0] == 'D'){
            scanf("%d",&x);
            deleteNode(x+1);
        }else if(op[1] == 'L'){
            int number;
            scanf("%d %d",&x,&number);
            insert(l[x+1],number);
        }else{
            int number;
            scanf("%d %d",&x,&number);
            insert(x+1,number);
        }
    }
    int i;
    for(i=r[0];i != 1;i = r[i]){
        printf("%d ",e[i]);
    }
    return 0;
}

    作者：gao79138
    链接：https://www.acwing.com/
    来源：本博客中的截图、代码模板及题目地址均来自于Acwing。其余内容均为作者原创。
    著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。