树与图的遍历

1. 树与图的遍历方式

    树与图的遍历方式有两种：深度优先遍历和宽度优先遍历。遍历过程跟之前所讲述的DFS和BFS类似，这里就不再细讲。可以将图的深度优先遍历和宽度优先遍历看做是特殊的深度优先搜索和宽度优先搜索。由于深度优先遍历和宽度优先遍历都会只遍历节点一次，因此时间复杂度是O(n+m),其中n表示节点数，m表示边数。

2. 有向图的深度优先遍历

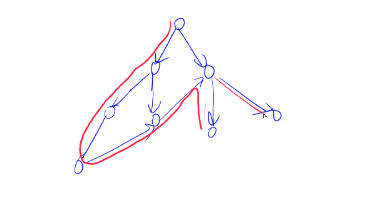
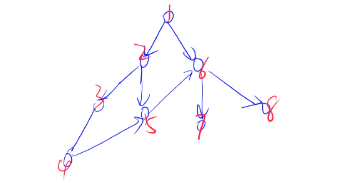
3. 有向图的宽度优先遍历

4. 深度优先遍历模板

int dfs(int u)
{
    st[u] = true; // st[u] 表示点u已经被遍历过

    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!st[j]) dfs(j);
    }
}

5. 宽度优先遍历模板

queue<int> q;
st[1] = true; // 表示1号点已经被遍历过
q.push(1);

while (q.size())
{
    int t = q.front();
    q.pop();

    for (int i = h[t]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!st[j])
        {
            st[j] = true; // 表示点j已经被遍历过
            q.push(j);
        }
    }
}

6. 深度优先遍历例题

https://www.acwing.com/activity/content/problem/content/909/

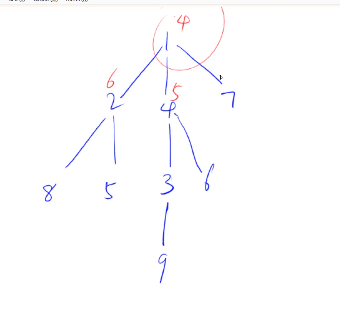
    我们用一张图来解释本题的题意。
    节点上面的数字表明：如果将这个节点删掉，则剩余的连通块中最多的节点个数。
    如果将1删掉，则剩余的连通块中最多的节点个数为4。
    如果将2删掉，则剩余的连通块中最多的节点个数为6。
    如果将4删掉，则剩余的连通块中最多的节点个数为5。
    ...
    最终的结果表明：只有将1删掉后，剩余的连通块中所包含的最多的节点个数是最小(相比于其余节点)的。因此重心为1。

    知道了上述的定义后，我们可以得出这道题的解题思路：
    1.  遍历每一个节点，求出删掉这个节点后，剩余的连通块中最多的节点个数。
    2.  从这些数中选择一个最小的，答案就出来了。
    那么，我们如何求出：删掉某个节点后，剩余的连通块中最多的节点个数？我们可以用深度优先遍历来解决这个问题。因为深度优先遍历可以求出遍历的子树中节点的个数。

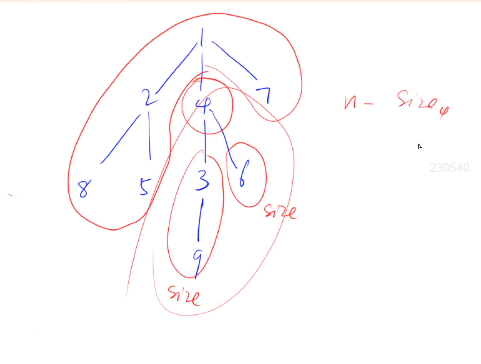
    我们举一个具体的例子，假设我们要删除上述4节点，求出剩余的连通块中最多的节点个数。
    1.  首先，将4这个节点删除后，我们可以得到如下连通块：以1为根的子树，以3为根的子树和以6为根的子树。 
    2.  其次，我们可以通过深度优先遍历来求出4这颗子树的节点个数以及以3为根的这颗子树的节点个数和以6为根的这颗子树的节点个数。
    3.  那么，以1为根的子树的节点个数怎么求？由于我们已经知道了以4为根的节点个数，那么我们只需要用：
    总节点个数-以4为根的节点个数
        就求得了以1为根的子树的节点个数。具体看上图即可。
    换句话说，在深度优先遍历的过程中，对于每一个节点，我们都可以算出：把该节点删除后，求出剩余的连通块的节点个数，找一个最大的即可。（删掉这个节点后，剩余的连通块中最多的节点个数。）这样的话，我们就可以根据上述的解题思路来解决问题了。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 100010;


//代表邻接表,其中h[N]代表头指针，e[2*N]代表节点值，ne[2*N]代表边，idx指向即将要用的节点。
int h[N],e[2*N],ne[2*N],idx = 0;

//代表当前节点是否已经遍历过
bool st[N];

//代表当前输入的节点总数
int n;

//代表最终答案，最小的最大值
int ans = N;
    
//往邻接表中添加一个边a->b
void add(int a,int b){
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}
//深度优先遍历
//返回以u为根的子树节点个数
int dfs(int u){
    //记录当前节点已被遍历
    st[u] = true;
    //sum代表以u为根的子树节点个数,从1开始代表算上当前节点
    int sum = 1;
    //res代表删除u节点后，剩余的连通块中最大的节点数量
    int res = 0;
    //遍历跟u邻接的节点
    for(int i = h[u];i!=-1;i = ne[i]){
        //如果当前节点没有被遍历过
        if(!st[e[i]]){
            //s代表u节点的子树的节点数量
            int s = dfs(e[i]);
            res = max(res,s);
            sum += s;
        }
    }
    //求出最后一个连通块的节点个数，取最大
    res = max(res,n-sum);
    //从各个最大中取最小
    ans = min(ans,res);
    
    return sum;
}




int main(){
    //将头指针初始化为-1
    scanf("%d",&n);
    memset(h,-1,sizeof(h));
    for(int i=0;i<n;i++){
        int a,b;
        scanf("%d%d",&a,&b);
        //无向图，添加两条有向边。
        add(a,b);
        add(b,a);
    }
    dfs(1);
    printf("%d",ans);
    return 0;
}

7. 宽度优先遍历例题

https://www.acwing.com/activity/content/problem/content/910/

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 100010;

int h[N],e[N],ne[N],idx = 0;

bool st[N];

int d[N];

int q[N];
int hh = 0,tt = -1;
int n,m;



void add(int a,int b){
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}

int bfs(){
    memset(d,-1,sizeof(d));
    d[1] = 0;
    st[1] = true;
    q[++tt] = 1;
    while(hh <= tt){
        int t = q[hh++];
        for(int i=h[t];i!=-1;i=ne[i]){
            if(!st[e[i]]){
                d[e[i]] = d[t] + 1;
                st[e[i]] = true;
                q[++tt] = e[i];
            }
        }
    }
    return d[n];
}



int main(){
    scanf("%d%d",&n,&m);
    memset(h,-1,sizeof(h));
    for(int i=0;i<m;i++){
        int a,b;
        scanf("%d%d",&a,&b);
        add(a,b);
    }
    printf("%d",bfs());
    return 0;
}

    作者：gao79138
    链接：https://www.acwing.com/
    来源：本博客中的截图、代码模板及题目地址均来自于Acwing。其余内容均为作者原创。
    著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。