二分图算法及模板
二分图算法及模板
1. 二分图算法要解决的问题

二分图算法要解决的问题有两个:
1. 用dfs来判断二分图(也称为染色法)。
2. 求二分图的最大匹配。(采用匈牙利算法)。
2. 染色法的基本思想
二分图的定义:
如果某一个图存在如下性质:
1. 可以将节点分为两个集合.
2. 节点之间的边都在集合之间,集合内部是没有边的。
满足如上性质的图,就称为二分图。
二分图的基本性质:
如果一个图是二分图,当且仅当图中不含奇数环。其中,奇数环的定义为:环路,边数为奇数。
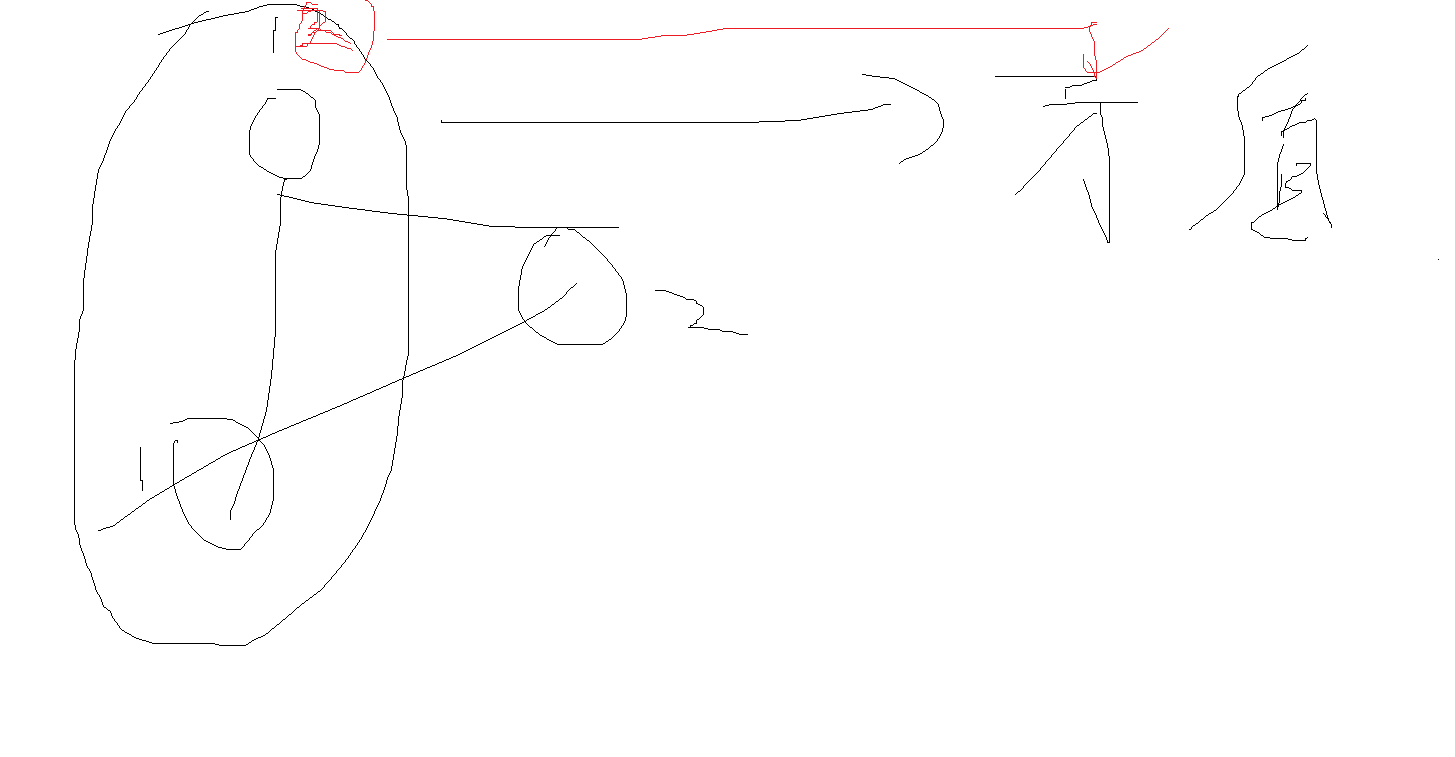
下面对如上的性质进行简单的证明:
如果一个图中含有奇数环,那么边数一定为奇数,节点数一定为偶数个。又因为,这个图是一个环,所以在偶数点当中一定有两个点相等。因此,实际存在的点只有奇数个。那么在进行染色的过程中,假设我们选取x号点作为1颜色。遍历x号点的所有邻接点,只能将其设定为2颜色。(根据二分图的定义,如果存在a-b这条边,a属于1集合,b只能属于2集合。集合之间可以存在边,集合内不允许有边)再遍历x号点的邻接点的邻接点,将其设定为1颜色....。由于节点个数只有奇数个,边数也为奇数,构成环路,那么在对其进行染色的过程中,一定会有一个点既被染成1颜色也被染成2颜色。这样的话,就矛盾了。请见上图。
上图中,第一个点既被染成了1颜色,也被染成了2颜色。这就是冲突的情况。因此,如果图中含有奇数环,那么这个图一定不是二分图。
我们根据上述的例子,观察到:如果在染色的过程中,出现了冲突的情况,那么这个图一定不是二分图。同理,如果在染色的过程中,没有出现冲突,那么这个图一定就是二分图。同时,我们也可以观察到:在进行染色的过程中,如果这个图是二分图的话,那么一个点与其邻接点的颜色一定相反,如果相同的话,一定冲突。(上述的图示也清楚的说明了这一点)因此,我们可以根据这样的性质来进行代码的编写。
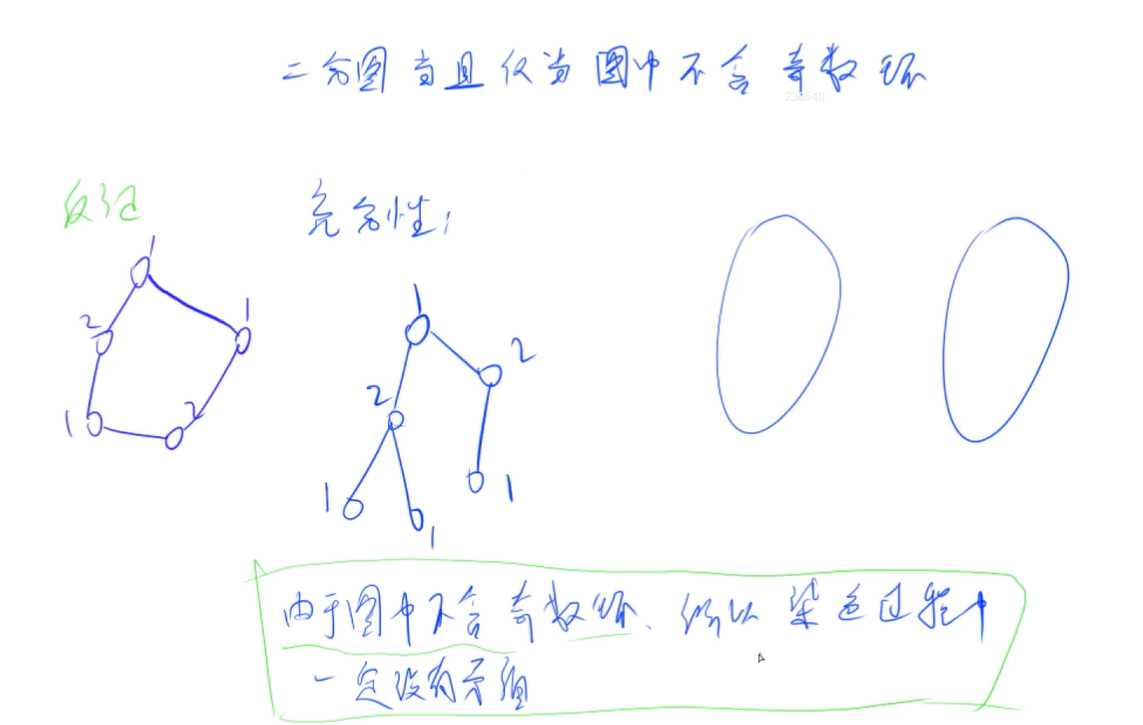

染色法的基本流程:
1. 首先遍历每一个点。
2. 在遍历点的过程中,利用dfs来对点进行染色。这样做的效果就是:该点所在的连通块都会进行染色。
3. 如果该点(a)没有进行染色的话,那么为其指定一个初始颜色(假设这里是1)。然后通过dfs找到它的邻接点(b)。
4. 如果a的临界点b也没有进行染色的话,那么为其指定颜色。(如果a是1,那么b就是2)指定颜色之后,再通过dfs进行遍历,直到将其连通块都染上色为止。
5. 在染色的过程中,可能会出现如下情况:
5.1 所有节点都正常进行染色,没有发生冲突,那么就代表此图为二分图。
5.2 如果在染色的过程中,发生了冲突,那么代表此图不是二分图。
3. 染色法的模板
int n; // n表示点数
int h[N], e[M], ne[M], idx; // 邻接表存储图
int color[N]; // 表示每个点的颜色,-1表示未染色,0表示白色,1表示黑色
// 参数:u表示当前节点,c表示当前点的颜色
bool dfs(int u, int c)
{
color[u] = c;
for (int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if (color[j] == -1)
{
if (!dfs(j, !c)) return false;
}
else if (color[j] == c) return false;
}
return true;
}
bool check()
{
memset(color, -1, sizeof color);
bool flag = true;
for (int i = 1; i <= n; i ++ )
if (color[i] == -1)
if (!dfs(i, 0))
{
flag = false;
break;
}
return flag;
}
4. 染色法的例题
https://www.acwing.com/problem/content/862/
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int N = 100010;
const int M = 200010;
int e[M],ne[M],h[N],idx = 0;
int n,m;
//代表该点的颜色
int color[N];
void add(int a,int b){
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
//u代表节点,c代表颜色
bool dfs(int u,int c){
//将该点进行染色
color[u] = c;
//遍历该点的邻接点
for(int i=h[u];i!=-1;i=ne[i]){
int j = e[i];
//如果邻接点没有染色
if(!color[j]){
//进行染色,如果染色过程中,没有发生冲突,返回true,否则返回false
//染色过程中,发生了冲突
if(!dfs(j,3-c)){
return false;
}
}else{
//如果该点已经染色了,判断:
//如果某点与其邻接点的颜色相同,那么冲突了
if(color[u] == color[j]){
return false;
}
}
}
return true;
}
int main(){
memset(h,-1,sizeof(h));
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
int a,b;
scanf("%d%d",&a,&b);
add(a,b);
add(b,a);
}
//代表图是否为二分图(1颜色和2颜色)
bool flag = true;
for(int i=1;i<=n;i++){
//如果该点没有进行染色的话
if(!color[i]){
//dfs的返回值代表染色过程中,是否发生了冲突,如果没有发生冲突,true,反之为false。
if(!dfs(i,1)){
//发生冲突,该图不是二分图
flag = false;
break;
}
}
}
if(flag == true){
printf("Yes");
}else{
printf("No");
}
return 0;
}
5. 匈牙利算法的基本思路
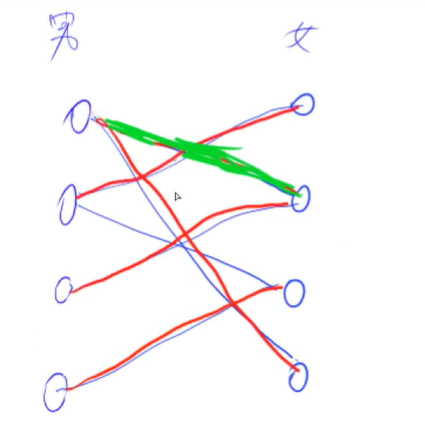
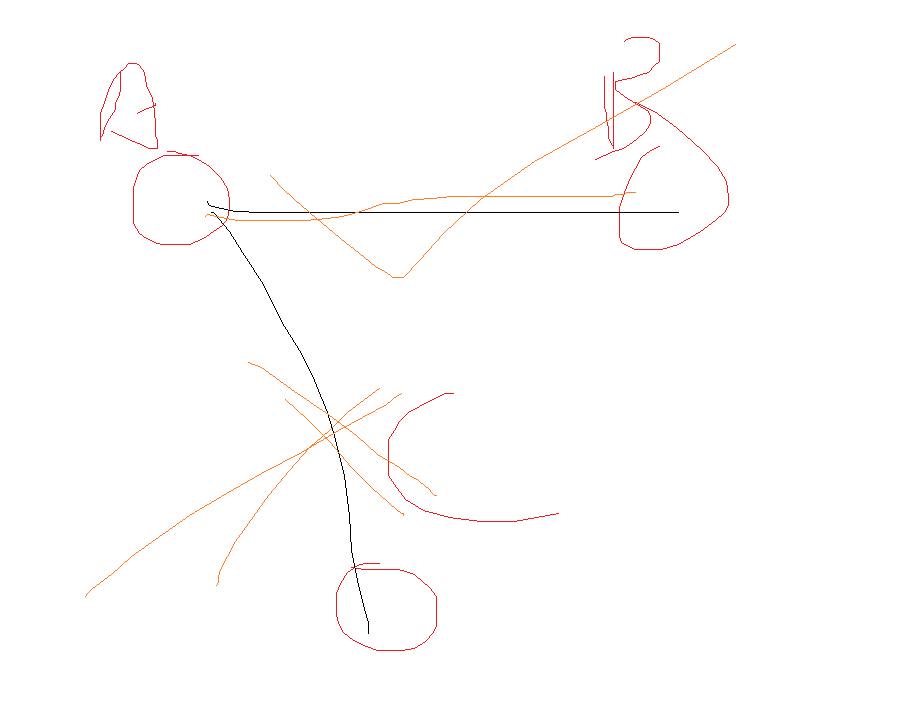
匈牙利算法用于求二分图的最大匹配。所谓二分图的最大匹配就是指:
在给定的二分图下,寻找到这样的一条边(匹配)。边上的两个节点均满足除了这条边(匹配)之外,没有别的边(匹配)指向自己或从自己发出。这样的边就称之为二分图的一个匹配。匈牙利算法的目的就是求二分图中最大能有多少个这样的边。这就是二分图的最大匹配问题。
对应于上述的图,红色就是匹配,绿色或没有颜色就是不匹配。上图的最大匹配为4。
举一个例子:如果节点a和节点b邻接,节点a与节点c邻接。意味着有两条边:a-b,a-c。那么,如果a和b构成了匹配,那么a-c这条边就不是匹配。因为,a已经和b匹配了,a不能在跟c匹配。
匈牙利算法的证明是非常困难的,这里不进行讲述。想知道的,可以参考算法导论这本书。
给定一个二分图,匈牙利算法的执行过程如下:
1. 对某一个集合的节点进行遍历。
2. 在遍历的过程中,假设遍历的点为x,找到x所邻接的点a。这时会有如下情况:
3.1 所邻接的点a还没有匹配,那么构成匹配,遍历下一个点(x+1)即可。
3.2 所邻接的点a已经匹配了,那么查看a所匹配的点b是否还有其余的点可以跟它构成匹配。
3.2.1 如果存在这样的点c可以与b匹配,那么进行b与c匹配,x与a匹配即可。
3.2.2 如果不存在这样的点c可以与b匹配,那么维持a与b的匹配。
继续查看x是否还有其余邻接的点,反复进行上述操作。如果到最后仍是没有节点
与x匹配,那么放弃x的匹配,遍历下一个点(x+1)即可。
3. 在构成匹配的时候,需要进行计数操作,当算法执行完毕之后,输出累加的数量,这就是二分图的最大匹配。我们利用匈牙利算法就可以求出一个二分图的最大匹配。
6. 匈牙利算法的模板
int n1, n2; // n1表示第一个集合中的点数,n2表示第二个集合中的点数
int h[N], e[M], ne[M], idx; // 邻接表存储所有边,匈牙利算法中只会用到从第一个集合指向第二个集合的边,所以这里只用存一个方向的边
int match[N]; // 存储第二个集合中的每个点当前匹配的第一个集合中的点是哪个
bool st[N]; // 表示第二个集合中的每个点是否已经被遍历过
bool find(int x)
{
for (int i = h[x]; i != -1; i = ne[i])
{
int j = e[i];
if (!st[j])
{
st[j] = true;
if (match[j] == 0 || find(match[j]))
{
match[j] = x;
return true;
}
}
}
return false;
}
// 求最大匹配数,依次枚举第一个集合中的每个点能否匹配第二个集合中的点
int res = 0;
for (int i = 1; i <= n1; i ++ )
{
memset(st, false, sizeof st);
if (find(i)) res ++ ;
}
7. 匈牙利算法的例题
https://www.acwing.com/problem/content/863/
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int N = 510;
const int M = 100010;
int h[N],e[M],ne[M],idx = 0;
//代表某个节点所匹配的点
int match[N];
//如果某一个节点考虑过了,那么就不再进行考虑
//存储某一个节点是否已经考虑过。
bool st[N];
int n1,n2,m;
void add(int a,int b){
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
bool find(int x){
//遍历x的所有邻接点
for(int i=h[x];i!=-1;i=ne[i]){
int j = e[i];
//如果邻接点j没有考虑过
if(!st[j]){
//考虑这个点
st[j] = true;
//如果j没有进行匹配或j进行了匹配,但j所匹配的点找到了其他的匹配。
if(match[j] == 0 || find(match[j])){
//将x和j进行匹配
match[j] = x;
return true;
}
}
}
//如果遍历了x的所有邻接点,发现都无法跟x匹配
//x匹配失败
return false;
}
int main(){
memset(h,-1,sizeof(h));
scanf("%d%d%d",&n1,&n2,&m);
for(int i=1;i<=m;i++){
int a,b;
scanf("%d%d",&a,&b);
add(a,b);
}
//代表最大匹配数量
int res = 0;
//从n1集合中,开始匹配
for(int i=1;i<=n1;i++){
//由于每次进行匹配的时候,情况都不一样,因此每次都要重置st数组。具体可以看博客的图例。
memset(st,false,sizeof(st));
//从节点i开始进行匹配,如果i匹配成功(find(i)的返回值为true),那么将匹配的数量+1。如果为false,则不进行操作。
if(find(i)){
res++;
}
}
printf("%d",res);
return 0;
}
作者:gao79138
链接:https://www.acwing.com/
来源:本博客中的截图、代码模板及题目地址均来自于Acwing。其余内容均为作者原创。
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。