Noblesse Code补题

题意:给你n个pairs,然后再有q次询问,每次询问给一个A,B。然后对于A,B,你可以无限次的进行两种操作,这两种操作分别是把(a,b)变成(a+b,b)或者(a,a+b),然后你要求的是对于a,b,你能通过这些操作变成原本给出的n个pairs中的多少个,每次询问输出个数。
做法:赛中的时候,我模拟了半天,发现要倒着做,从n个开始想。对于一个pairs,变化有三种情况:
一,两者一样大,这时候就没有上一步了,要注意到给出的AB都是大于等于1的。这时候,他就是最原始的那个pair,只有他变成别人,没有别人变成他
二,A比B大,那么他的上一步一定是A-B,B。为什么?因为如果是A,B-A的话就又有负数了!
三,B比A大,同上。
然后我们可以发现,这是操作树。
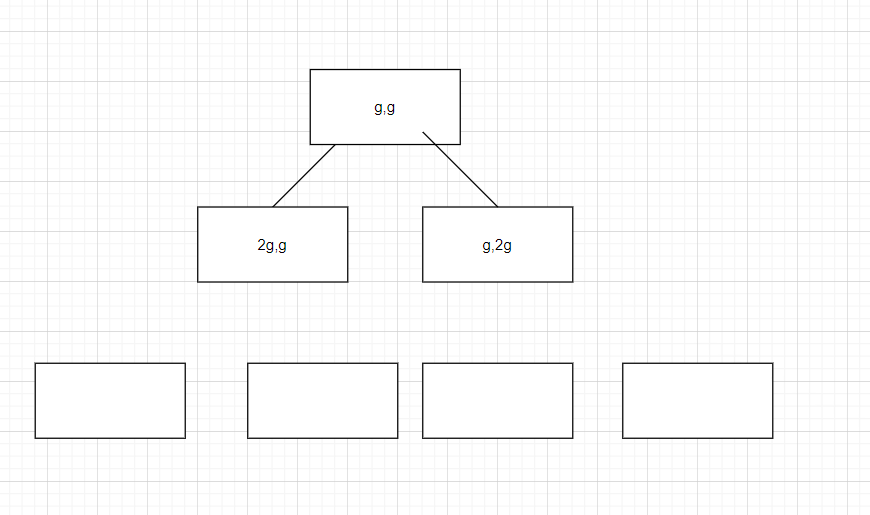
向上的路径是唯一的,向下的路径是两条的,这不就是二叉树?然后我们发现,这就是模拟一个辗转相除法,根节点就是gcd。
比赛的时候就卡住了,一开始我一位只要gcd相同就好了,但是他会有那种同根不同路径的情况,而合法的情况中,AB必然在能生成的ab的生成的路径作为一个节点。也就是说AB一定得是ab的爹或爷爷,y染色体都得相同的。
之后看题解,哦那是真的牛批。他把对于每种gcd,做一个vector,里面存放从根节点生成他的路径,然后在这个vector中,对AB生成的路径进行二分,然后通过两次二分把他能生成的节点给求出来。第一次二分check为他本身,那么比他小的定然不能生成。第二次二分check为他加上一个大一点的字符,那么比他大的也定然不能生成,因为分叉都不一样了。然后一减就好了。
#include<bits/stdc++.h> #define de cout<<111<<"\n"; #define fi first #define se second #define int long long #define kx(a,b) ((a*b)%mod) #define kplus(a,b) ((a+b)%mod) #define lson k<<1,l,mid #define rson k<<1|1,mid+1,r #define ll k<<1 #define rr k<<1|1 #define lowbit(x) x&(-x); using namespace std; const int maxn=1000010; const int mod=998244353; //const int mod=1000000007; typedef pair<int,int> pii; int fect[maxn], infect[maxn]; int binpow(int a,int b,int m){ a%=m; int res=1; while (b > 0){ if (b & 1)res = res * a % m; a=a*a%m; b>>=1; } return res; } int C(int a,int b){ return fect[a]*infect[b]%mod*infect[a-b]%mod; } void initzuhe(int n){ fect[0]=1;infect[0]=1; for(int i=1;i<=n;i++){ fect[i]=(fect[i-1]*i)%mod; } infect[n-1]=binpow(fect[n-1],mod-2,mod); for(int i=n-2;i>=1;i--) infect[i]=infect[i+1]*(i+1)%mod; } int gcd(int a,int b){ if(b==0)return a; return gcd(b,a%b); } namespace trie { int next[maxn][26],cnt; bool vis[maxn],exist[maxn]; void init() { memset(next,0,sizeof(next)); cnt=1; } void insert(const string &s) { int cur=1; for(auto c:s) { if(!next[cur][c-'a']) next[cur][c-'a']=++cnt; cur=next[cur][c-'a']; } exist[cur]=true; } int find(const string &s) { int cur=1; for(auto c:s) { if(!next[cur][c-'a']) return 0; cur=next[cur][c-'a']; } if(exist[cur])return 1; return 0; } } const int N=1e5+10; int seg[N<<2]; int lazy[N<<2]; void build(int k,int l,int r) { if(l==r) { cin>>seg[k]; return ; } int mid=l+r>>1; build(lson); build(rson); seg[k]=seg[ll]+seg[rr]; return ; } void pushdown(int k,int l,int r) { if(l==r)return ; lazy[ll]+=lazy[k]; lazy[rr]+=lazy[k]; int mid=l+r>>1; seg[ll]+=lazy[k]*(mid-l+1); seg[rr]+=lazy[k]*(r-mid); lazy[k]=0; return ; } void update(int k,int l,int r,int x,int y,int z) { pushdown(k,l,r); if(x<=l&&y>=r) { seg[k]+=z*(r-l+1); lazy[k]+=z; return ; } int mid=l+r>>1; if(x<=mid) update(lson,x,y,z); if(y>mid) update(rson,x,y,z); seg[k]=seg[ll]+seg[rr]; } int quire(int k,int l,int r,int x,int y) { pushdown(k,l,r); if(x<=l&&y>=r) return seg[k]; int res=0ll; int mid=l+r>>1; if(x<=mid) res+=quire(lson,x,y); if(y>mid) res+=quire(rson,x,y); return res; } int n; int tree[500010]; void update(int x,int k){ while(x<=n){ tree[x]+=k; x+=lowbit(x); } } int sum(int x){ int res=0; while(x>=1){ res+=tree[x]; x-=lowbit(x); } return res; } bool isprime(int num) { if(num==1||num==4) return 0; if(num==2||num==3) return 1; if(num %6!= 1&&num %6!=5) return 0 ; int tmp =sqrt(num); for(int i=5;i<=tmp;i+=6) { if(num%i==0||num%(i+2)==0) return 0 ; } return 1 ; } typedef pair<string,vector<int>> pp; void get(int a,int b,pp&s){ if(a==b)return ; if(a>b){ if(a%b==0){ int k=a/b-1; s.fi+="l"; s.se.push_back(k); return ; } int k=a/b; s.fi+="l"; s.se.push_back(k); get(a-k*b,b,s); return ; } else{ if(b%a==0){ int k=b/a-1; s.fi+="r"; s.se.push_back(k); return ; } int k=b/a; s.fi+="r"; s.se.push_back(k); get(a,b-k*a,s); return ; } } bool cmp(pp &a, pp &b) { int i=0,j=0; int li=0,lj=0; int n=a.fi.size(), m=b.fi.size(); string &s =a.fi, &t =b.fi; vector<int>&nums=a.se, &numt=b.se; if (i<n&&j<m){ li=nums[i]; lj=numt[j]; } while(i<n&&j<m){ if (s[i]<t[j])return true; else if (s[i] > t[j]) return false; if(li==lj){ i++; j++; if(i<n&&j<m){ li = nums[i]; lj = numt[j]; } } else if (li<lj){ i++; if(i<n){ if(s[i]<t[j])return true; else if(s[i]>t[j]) return false; } } else{ j++; if(j<m){ if(s[i]<t[j])return true; else if(s[i]>t[j])return false; } } } if(j==m)return false; else return true; } vector<pp>arr[50010]; void solve(){ map<int,int>c; int n,q,cnt=0ll;cin>>n>>q; for(int i=0;i<n;i++){ int a,b;cin>>a>>b; int g=gcd(a,b); if(!c[g]){ c[g]=++cnt; arr[cnt].clear(); } pp temp;get(a,b,temp); reverse(temp.fi.begin(), temp.fi.end()); reverse(temp.se.begin(), temp.se.end()); arr[c[g]].push_back(temp); } for(int i=1;i<=cnt;i++){ sort(arr[i].begin(),arr[i].end(),cmp); } while(q--){ int a,b;cin>>a>>b; int g=gcd(a,b); if(!c[g]){ cout<<0<<"\n"; continue; } g=c[g]; pp temp;get(a,b,temp); reverse(temp.fi.begin(), temp.fi.end()); reverse(temp.se.begin(), temp.se.end()); int l=0,r=(int)arr[g].size(); while (l<r) { int mid=l+r+1>>1; if (cmp(arr[g][mid - 1],temp))l = mid; else r=mid - 1; } int tem=l; l=0, r=(int)arr[g].size(); temp.fi+='s';temp.se.push_back(1); while (l<r){ int mid=l+r+1>>1; if(cmp(arr[g][mid-1],temp))l=mid; else r=mid-1; } cout<<l-tem<<"\n"; } } signed main(){ std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0); int t;cin>>t;while(t--) solve(); }