学不会的图论——存储篇

clear_tea / 2023-08-29 / 原文

前言

来填博弈论图上删边游戏的坑了~~（绝对不是因为杭电杯的题太难了补不出来）~~，学习缩点之前，肯定要把图论的知识点基础知识先学学清楚啦ヾ(≧▽≦*)o

邻接矩阵

学过离散数学的同学都知道，可以直接用矩阵来存图，我们不妨定义 graph[N][N] ，如果i，j直接相连，用graph[i][j]表示边权，否则将graph[i][j]赋值为INF，举个例子（$V_i$表示点，$E_i$表示边权）

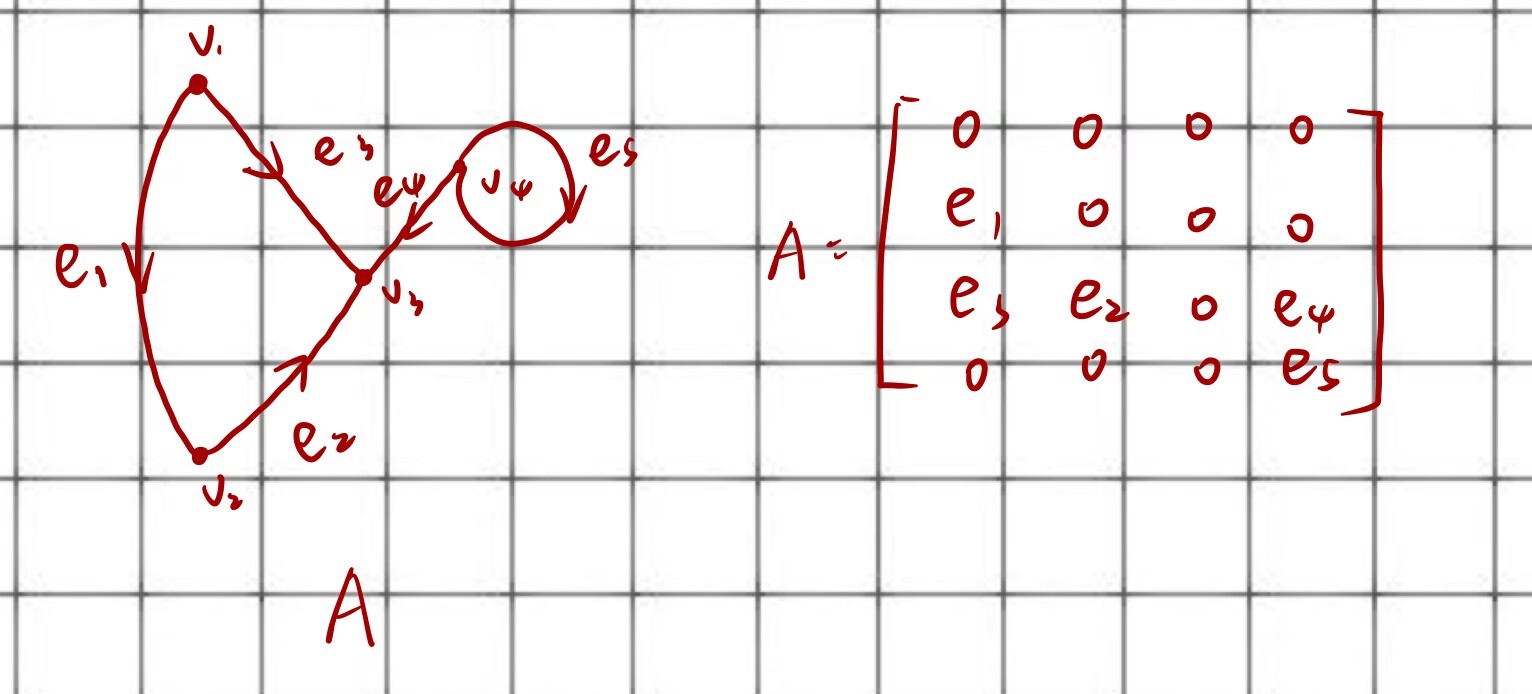
上图是有向边的例子，如果是无向边的话，让graph[i][j] = graph[j][i] = $E_i$

优点

1、简单直接、编程极简
2、查找边（i，j）非常快，复杂度为O(1)
3、适合稠密图

缺点

1、表示稀疏图会造成大量的空间浪费
2、不能存储重边

我的代码

#include <bits/stdc++.h>
#define int long long
const int N = 1e5 + 5;
const int inf = 0x3f3f3f3f3f3f3f3f;
int graph[N][N];
signed main(){
    for(int i = 0;i < N;i ++){
        for(int j = 0;j < N;j ++){
            graph[i][j] = inf;
        }
    }
    int n;
    std::cin >> n;
    for(int i = 1;i <= n;i ++){
        int u,v,w;
        std::cin >> u >> v >> w;
        graph[u][v] = w;
    }
    return 0;
}

邻接表

我们已经知道了邻接矩阵在存储稀疏图的时候会造成大量的空间浪费，所以我们可以使用邻接表来存储稀疏图。在邻接表中，我们只存储直接相连的两个节点，不存储不相连的两个节点

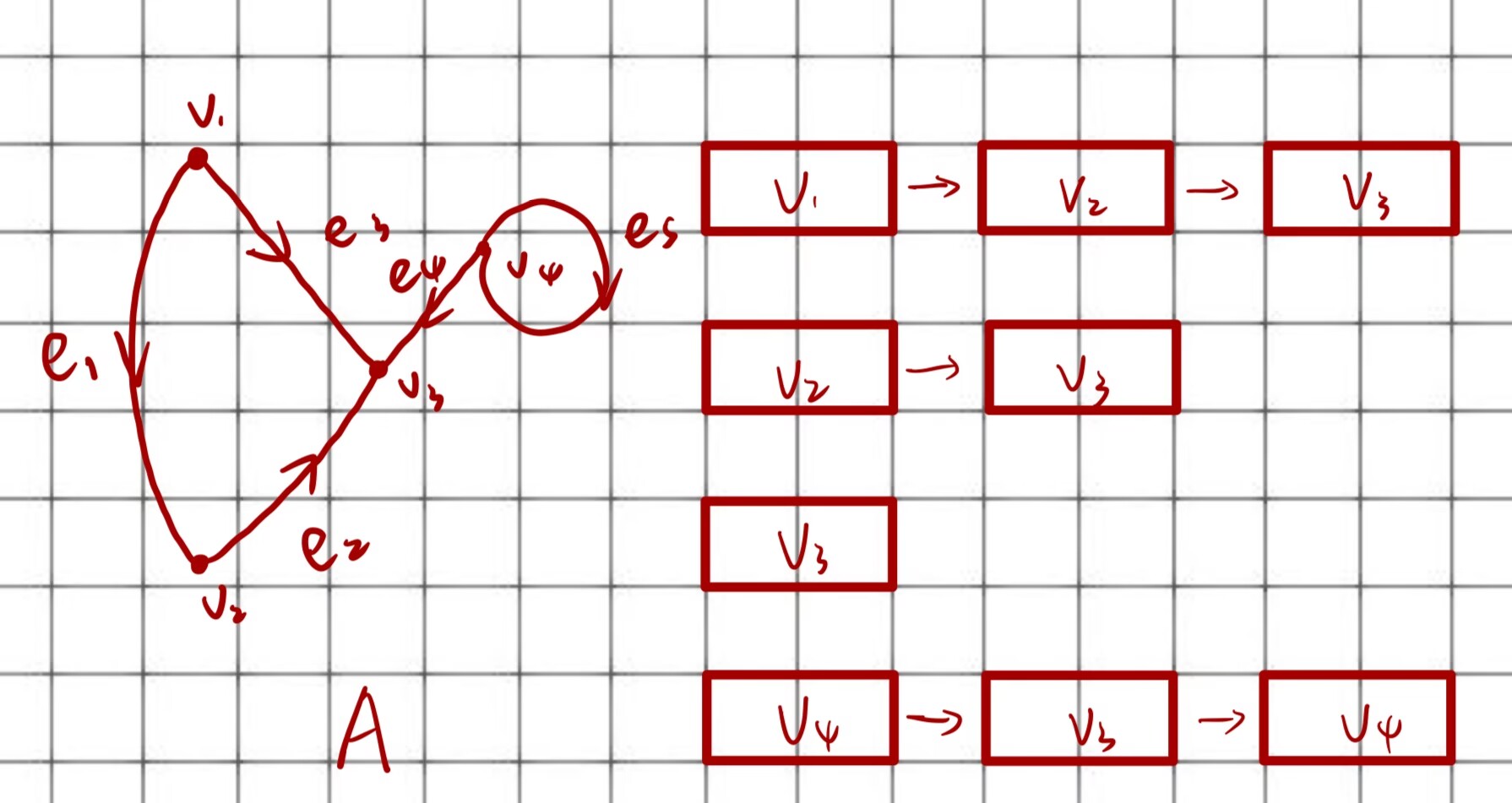
缺点

1、找到一个节点的一个相邻节点需要遍历全部节点

我的代码

#include <bits/stdc++.h>
#define int long long
const int N = 1e5 + 5;
struct edge{
    int from,to,w;
    edge(int a,int b,int c){
        from = a;
        to = b;
        w = c;
    }
};
std::vector<edge> e[N];
signed main(){
    int n;
    std::cin >> n;
    for(int i = 1;i <= n;i ++) e[i].clear();

    for(int i = 1;i < n;i ++){
        int u,v,w;
        std::cin >> u >> v >> w;
        e[u].push_back({u,v,w});
    }
    return 0;
}

链式前向星

从前面的部分，我们不难知道，邻接表是，存储一个节点u的邻接边，其方法的关键是先定位第1条边，第1条边再指向第2条边，第2条边再指向第3条边……

我们不妨设置以下结构：

1、一个head[ ]数组，head[u]表示以u作为起点的第一条边的编号。

2、一个结构体

struct edge {
    int next;
    int to;
    //int w;
};

edge的下标cnt表示编号，edge[cnt].to表示节点的名称，edge[cnt].next表示这个节点的下一个点的编号，如果需要的话，edge[cnt].w表示由edge[cnt]表示的边的权值。

我们用下面这张图来理解一下

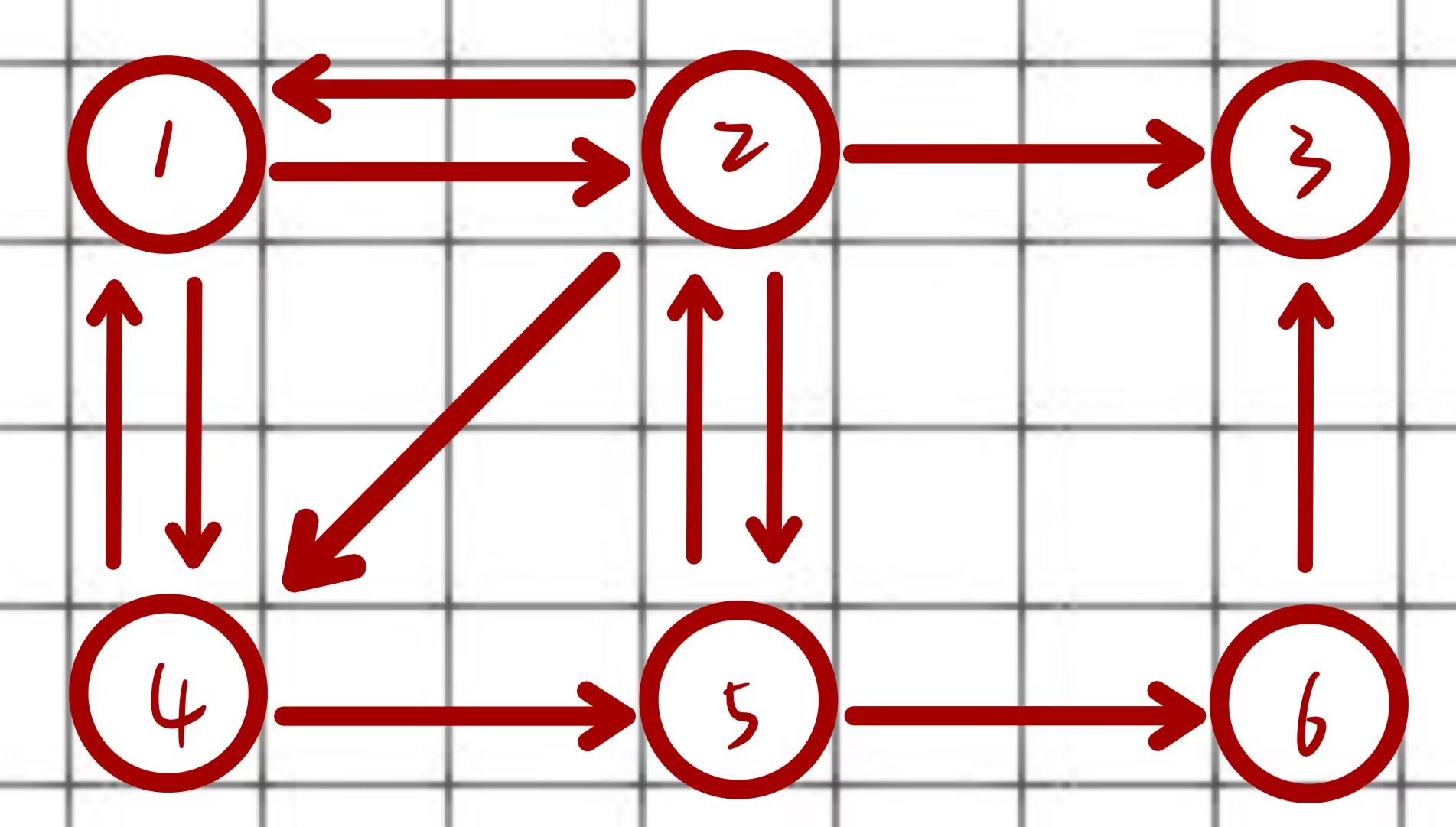
用链式前向星存图能得到下面的结果

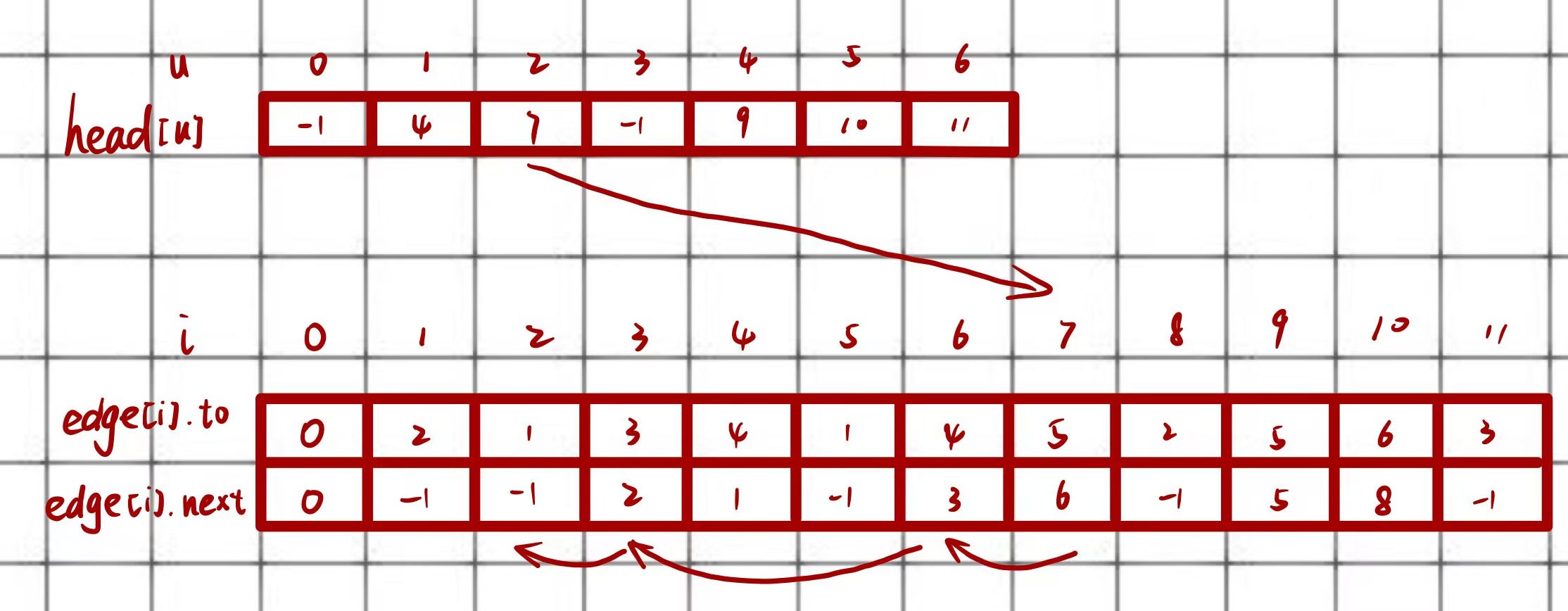
其中，我们以2号节点为例

1、head[2] = 7，说明2号节点的第一条边存储在edge[7]

2、edge[7].to = 5，edge[7].next = 6，说明2 -> 5有一条边，2号节点的下一条边存储在edge[6]

3、重复上述，直到edge[2].next = -1，则表示以2号节点为起点的有向边已经全部找到

4、如果head[u] = -1，说明没有以u为起点的有向边

下面给出链式前向星存图的代码~~（绝对不是懒得再说了！）~~

#include<bits/stdc++.h>
#define int long long
const int N = 1e5 + 5;
struct Edge{
    int to;
    int next;
}edge[N];
int head[N];
int cnt = 0;
void add(int u , int v){
    edge[++ cnt].next = head[u];
    edge[cnt].to = v;
    head[u] = cnt;
}
void solve(){
    std::memset(head , - 1 , sizeof(head));
    cnt = 0;
    int n , m;
    std::cin >> n >> m;
    for(int i = 1; i <= m ; i ++){
        int u , v;
        std::cin >> u >> v;
        add(u,v);
    }
}
signed main(){
    std::ios::sync_with_stdio(0);
    std::cin.tie(0);std::cout.tie(0);

    int t = 1;
//    std::cin >> t;
    while (t --){
        solve();
    }

    return 0;
}