[ABC317G] Rearranging 题解
取自我的洛谷博客:https://www.luogu.com.cn/blog/SunnyYuan/solution-at-abc317-g
借鉴了官方题解思路。
思路
首先我们要建立一个二分图。
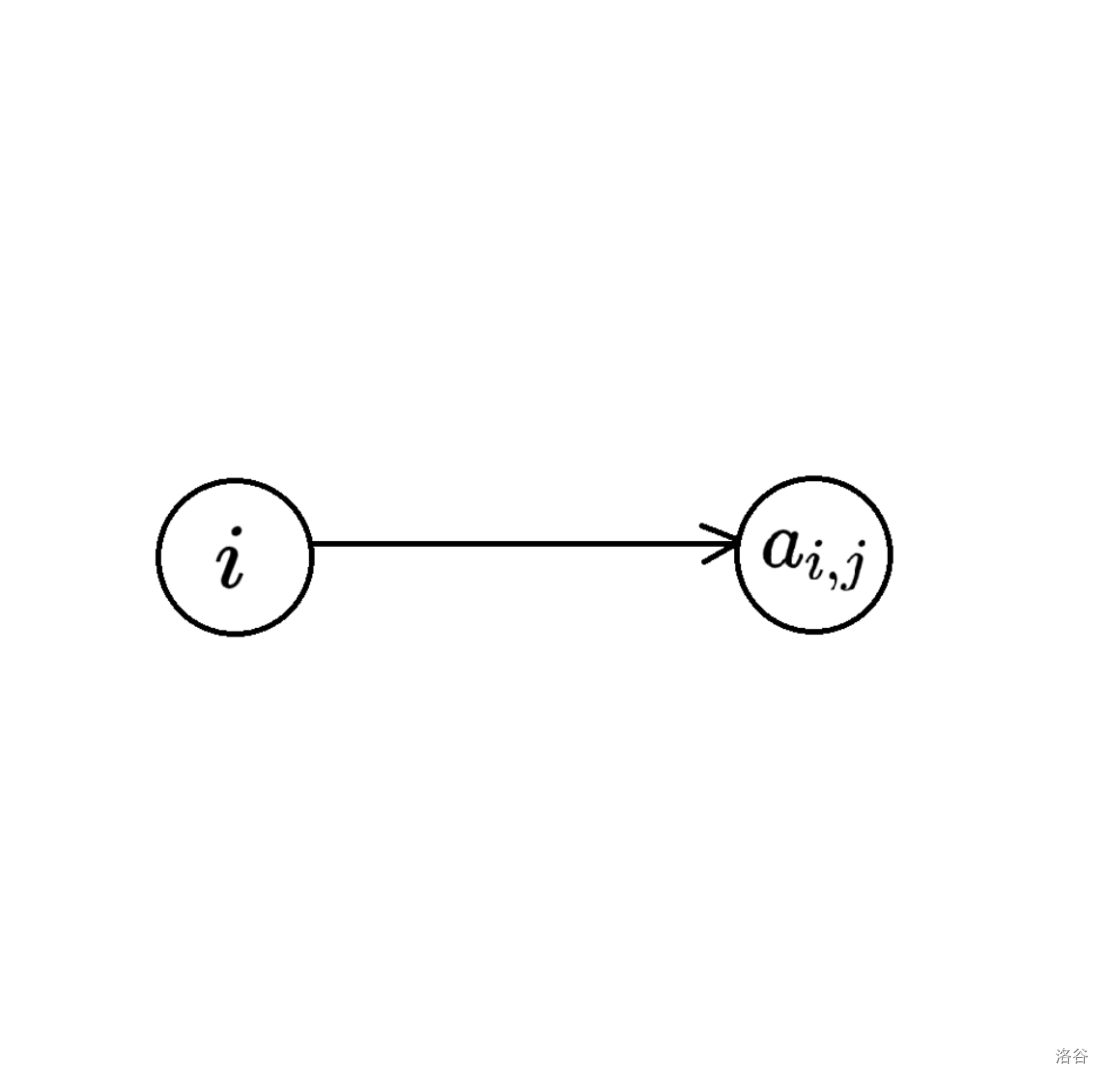
对于输入的 \(a_{i, j}\),我们可以连接 左侧的 \(i\) 和 右侧的 \(a_{i, j}\)。
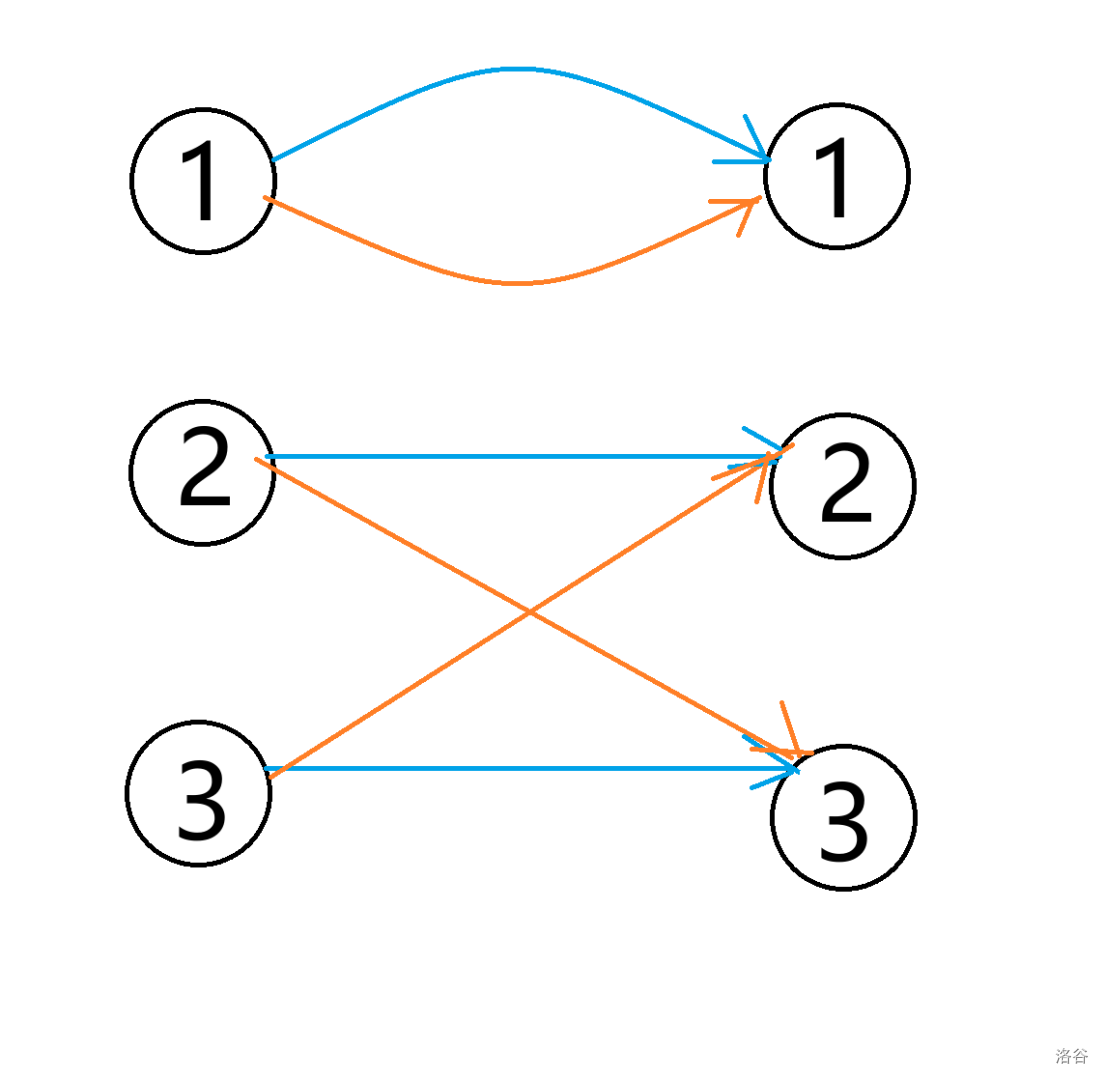
比如样例 \(1\):
注意:左边的 \(1, 2, 3\) 和 右边的 \(1, 2, 3\) 完全不一样,一个是行数,一个是数字。
-
那我们现在找出一组二分图的最大匹配,那么就代表对于固定的一列,第 \(i\) 行的数字就可以确定了。
比如上图中橙色的边,它们就是一组二分图的最大匹配,我们可以通过其知道对于一列,可以这么填:
\[\begin{aligned}
1\\
3\\
2\\
\end{aligned}
\]
-
我们将已经匹配的边删去,然后再跑下一次的二分图,构建下一列的数字。就这样执行 \(m\) 遍,就可以做出答案。

可以得到最大匹配,然后构建出这一列数字:
\[\begin{aligned}
1\\
2\\
3\\
\end{aligned}
\]
- 最后将这么多列数字按任意顺序输出就可以了。
\[\begin{aligned}
\text{1 1}\\
\text{2 3}\\
\text{3 2}\\
\end{aligned}
\]
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 210, M = 40010, INF = 0x3f3f3f3f;
struct edge {
int to, next, w;
} e[M];
int head[N], idx = 1;
void add(int u, int v, int w) {
idx++, e[idx].to = v, e[idx].next = head[u], e[idx].w = w, head[u] = idx;
idx++, e[idx].to = u, e[idx].next = head[v], e[idx].w = 0, head[v] = idx;
}
int S, T;
int n, m;
int q[N], hh, tt;
int d[N];
int ans[N][N];
bool bfs() {
memset(d, 0, sizeof(d));
hh = tt = 0;
q[0] = S;
d[S] = 1;
while (hh <= tt) {
int u = q[hh++];
for (int i = head[u]; i; i = e[i].next) {
int to = e[i].to;
if ((!d[to]) && e[i].w) {
d[to] = d[u] + 1;
q[++tt] = to;
}
}
}
return d[T];
}
int dinic(int u, int limit) {
if (u == T) return limit;
int rest = limit;
for (int i = head[u]; i && rest; i = e[i].next) {
int to = e[i].to;
if (d[to] == d[u] + 1 && e[i].w) {
int k = dinic(to, min(rest, e[i].w));
if (!k) d[to] = INF;
rest -= k;
e[i].w -= k;
e[i ^ 1].w += k;
}
}
return limit - rest;
}
int maxflow() {
int ans = 0, flow = 0;
while (bfs()) while (flow = dinic(S, INF)) ans += flow;
return ans;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
S = 0, T = n << 1 | 1;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
int x;
cin >> x;
add(i, x + n, 1);
}
}
int tmp = idx;
for (int i = 1; i <= n; i++) add(S, i, 1), add(i + n, T, 1);
for (int j = 1; j <= m; j++) {
if (maxflow() != n) {
cout << "No\n";
return 0;
}
for (int i = 3; i <= tmp; i += 2) if (e[i].w == 1) {
int u = e[i].to, v = e[i ^ 1].to;
ans[u][j] = v - n;
e[i].w = e[i ^ 1].w = 0;
}
for (int i = tmp + 2; i <= idx; i += 2) {
if (e[i].w == 1) {
e[i ^ 1].w = 1;
e[i].w = 0;
}
}
}
cout << "Yes\n";
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cout << ans[i][j] << ' ';
}
cout << '\n';
}
return 0;
}