acm竞赛板子（自用）
月影几度凉的板子
基础算法
前缀和与差分
二维前缀和
如图所示，左边红框中所有数字的和
\[S[i][j]=S[i-1][j]+S[i][j-1]-S[i-1][j-1]+a[i][j]
\]
左边红框中子矩阵的数字和为
\[S[x_2][y_2]-S[x_1-1][y_2]-S[x_2][y_1-1]+S[x_1-1][y_1-1]
\]
二维差分
对二维前缀和的逆运算，核心操作:
int a[N][M];//差分数组
void insert(int x1,int y1,int x2,int y2,int c){
a[x1][y1]+=c;
a[x1][y2+1]-=c;
a[x2+1][y1]-=c;
a[x2+1][y2+1]+=c;
}
离散化
保序离散化
初始化
int q[N],a[N];
for(int i=0;i<n;i++) scanf("%d",&a[i]);
memcpy(q,a,sizeof q);
sort(q,q+n);
m=unique(q,q+n)-q;
查询原数组中某个元素对应的映射后的位置
int x=lower_bound(q,q+m,a[i])-q+1;
高精度计算
vector版本
加法
vector<int> add(vector<int> &A,vector<int> &B) {
vector<int> C;
int t=0;
for (int i=0; i<A.size() || i<B.size(); i++) {
if (i < A.size()) t += A[i];
if (i < B.size()) t += B[i];
C.push_back(t%10);
t /= 10;
}
if (t) C.push_back(t);
return C;
}
减法
bool cmp(vector<int> &A,vector<int> &B) {
if (A.size() != B.size()) return A.size()>B.size();
for (int i=A.size()-1; i>=0; i--) {
if (A[i] != B[i]) {
return A[i]>B[i];
}
}
return true;
}
vector<int> sub(vector<int> &A,vector<int> &B) {
vector<int> C;
int t=0;
for (int i=0; i<A.size(); i++) {
t = A[i]-t;
if (i < B.size()) t -= B[i];
C.push_back((t+10)%10);
if (t < 0) t = 1;
else t = 0;
}
while (C.size()>1 && C.back()==0) C.pop_back();
return C;
}
int main() {
string a,b;
vector<int> A,B;
cin >> a >> b;
for (int i=a.size()-1 ; i>=0; i--) A.push_back(a[i]-'0');
for (int i=b.size()-1; i>=0; i--) B.push_back(b[i]-'0');
if (cmp(A,B)) {
auto C=sub(A,B);
for (int i=C.size()-1; i>=0; i--) printf("%d",C[i]);
} else {
auto C=sub(B,A);
printf("-");
for (int i=C.size()-1; i>=0; i--) printf("%d",C[i]);
}
return 0;
}
高精度乘低精
vector<int> mul(vector<int> &A,int b) {
vector<int> C;
int t=0;
for (int i=0; i<A.size() || t; i++) {
if (i < A.size()) t += A[i]*b;
C.push_back(t%10);
t /= 10;
}
return C;
}
高精度乘高精度
vector<int> mul(vector<int> &a,vector<int> &b) {
vector<int> c;
for (int i=0; i<a.size(); i++) {
for (int j=0; j<b.size(); j++) {
if (i+j < c.size()) c[i+j] += a[i]*b[j];
else c.push_back(a[i]*b[j]);
}
}
int t=0;
for (int i=0; i<c.size(); i++) {
t += c[i];
c[i] = t%10;
t /= 10;
}
while (t) {
c.push_back(t%10);
t /= 10;
}
while (c.size()>1 && c.back()==0) c.pop_back();
return c;
}
高精度除低精度
vector<int> div(vector<int> &A,int b,int &r) {
vector<int> C;
r = 0;
for (int i=A.size()-1; i>=0; i--) {
r = r*10+A[i];
C.push_back(r/b);
r %= b;
}
reverse(C.begin(),C.end());
while (C.size()>1 && C.back()==0) C.pop_back();
return C;
}
数学
快速幂
给定 n 组 \(a_i,b_i,p_i\)，对于每组数据，求出 \(a^b\ mod \ p\)的值。
思想是把\(a^b\)，拆成\(a^{b_02^0+b_12^1\dots+b_{log_k(b)}2^{log_k(b)}}\),每一步都取模，时间复杂度为\(O(log_p(b))\)
代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int qmi(int a,int b,int p){
if(p==1) return 0;
int res=1;
while(b){
if(b&1) res=(long long)res*a%p;
b/=2;
a=(long long)a*a%p;
}
return res;
}
int main()
{
int n;
cin>>n;
while(n--){
int a,b,p;
scanf("%d%d%d",&a,&b,&p);
cout<<qmi(a,b,p)<<endl;
}
}
快速幂求逆元
若整数 b，m 互质，并且对于任意的整数 a，如果满足 \(b|a\)，则存在一个整数 x，使得 \(a/b≡a\times x(mod\ m)\)，则称 x 为 b 的模 m 乘法逆元，记为 \(b^{-1}\ mod(m)\)
b 存在乘法逆元的充要条件是 b 与模数 m 互质。当模数 m 为质数时，\(b^{m−2}\) 即为 b 的乘法逆元。
证明：
\[a/b\equiv a\times b^{-1} \ \ mod(m)\\
a\equiv a\times b^{-1}\times b\\
b\times b^{-1}\equiv1\\
\text {由费马小定理} b^{m-1}\equiv1\ mod(m),\text{当m为质数}\\
b\times b^{-1}\equiv b^{m-1}\ mod(m)\\
b^{-1}\equiv b^{m-2}
\]
代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
int qmi(int a,int b,int p){
if(p==1) return 0;
int res=1;
while(b){
if(b&1) res=(LL)res*a%p;
a=(LL)a*a%p;
b/=2;
}
return res;
}
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++){
int a,p;
cin>>a>>p;
if(a%p==0) cout<<"impossible"<<endl;
else cout<<qmi(a,p-2,p)<<endl;
}
}
欧几里得算法
如果\(a|b,且a|c,\)，那么一定有\(a|b+c,\ \ \ \ a|x*b+y*c\)
定理 \((a,b)\)的最大公约数和\((b,a\%b)\)相同
证明 设(a,b)的公约数为d，a%b可以看作是\(a-[\frac{a}{b}]b\),可以把这个式子看作\(ax+by\)的形式，所以d也为\((b,a\%b)\)的公约数
对于右边，公约数\(d|b,\ \ d\ \ | a-[\frac{a}{b}]b\),可以把a看成\(bx+(a-[\frac{a}{b}]b)y\)的形式，同理可得d也为a的公约数，所以两边最大公约数相等
代码
int gcd(int a,int b){
return b?gcd(b,a%b):a;
}
类欧几里得算法
在\(O(log(n))\)的时间复杂度内，求出 \(\sum_{i=0}^{n} \frac{ai+b}{c}\) 的值,原理类似辗转相除法
i128 floor_sum(i128 a, i128 b, i128 c, i128 n)
{
i128 res = 0;
if (a >= c)
{
res += n * (n + 1) * (a / c) / 2;
a %= c;
}
if (b >= c)
{
res += (n + 1) * (b / c);
b %= c;
}
i128 m = (a * n + b) / c;
if (m == 0)
return res;
res += n * m - floor_sum(c, c - b - 1, a, m - 1);
return res;
}
欧拉函数相关，原根，阶
定义
证明
设N分解质因子的表达式为\(N=p_1^{a_1}p_2^{a_2}\dots p_m^{a_m}\) 在1~N中,\(p_i\)的倍数有\([\frac{N}{pi}]\),这些数与N有相同的质因子，显然不和N互质，同理\(p_i p_j\)的倍数也不和N互质，我们可以先让N个整数减去所有为\(p_1到p_m\)的倍数的数，即\(N-(N/p_1+N/p_2+\dots N/p_m)\),但是对于一个数，如果既是\(p_i\)的倍数，又是\(p_j\)的倍数，那么就会被减去两次，所以需要在加上这些数，即$N-(N/p_1+N/p_2+\dots N/p_m)+ \sum_{1\le i<j\le m}^{}N/(p_ip_j) \(,但是如果同时为\)p_i,p_j,p_k$的倍数的数又会被多加，需要再减去一次，由容斥原理可以得到
\[\phi(N)=N(1-\frac{1}{p_1}-\frac{1}{p_2}\dots -\frac{1}{p_n}+\frac{1}{p_1p_2}+\frac{1}{p_1p_3}\dots -\frac{1}{p_1p_2p_3}-\frac{1}{p_2p_2p_4}+(-1)^m\frac{1}{p_1p_2\dots p_m}
\]
观察发现就是上图中所给的式子
代码 时间复杂度\(O(\sqrt N)\)
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++){
int a;
cin>>a;
int res=a;
for(int i=2;i<=a/i;i++){
if(a%i==0){
res=res/i*(i-1);
while(a%i==0) a/=i;
}
}
if(a>1) res=res/a*(a-1);
cout<<res<<endl;
}
}
线性筛法求欧拉函数
按照线性筛的方法，从小到大求\(\phi(x)\),当质因子枚举到\(p_j\),枚举到数字i时，对于一个数\(p_ji\),有
\[\phi(p_ji) =
\begin{cases}
p_j\phi(i), & \text{if }i\%p_j=0 \\
\phi(i)p_j(1-\frac{1}{p_j}), & \text{if }i\%p_j\ne0
\end{cases}
\]
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 1e6+10;
int prime[N],cnt;
int eluer[N];
bool st[N];
void get_eluer(int n){
eluer[1]=1;
for(int i=2;i<=n;i++)
{
if(!st[i]) prime[cnt++]=i,eluer[i]=i-1;
for(int j=0;prime[j]<=n/i;j++){
st[prime[j]*i]=true;
if(i%prime[j]==0){
eluer[prime[j]*i]=eluer[i]*prime[j];
break;
}
eluer[prime[j]*i]=eluer[i]*(prime[j]-1);
}
}
}
int main()
{
int n;
cin>>n;
get_eluer(n);
LL res=0;
for(int i=1;i<=n;i++) res+=eluer[i];
cout<<res<<endl;
return 0;
}
欧拉定理
若a和n互质，则
\[a^{\phi(n)}\equiv 1 \ (mod\ n)
\]
证明：
设在1~n范围内，与n互质且两两不相等的数为\(b[1],b[2]\dots,b[\phi(n)]\),将每个数乘上a，得到\(a*b[1],a*b[2]\dots,a*b[\phi(n)]\),对于任意一个\(a*b[j],1\le j\le \phi(n)\),因为a和\(b[j]\)都和n互质，所以他们的乘积也和n互质
下面证明一个推论，\(（a*b[j])mod\ n\)也和n互质
设\(a*b[j]\)模n的余数为t，假设t不和n互质，那么就存在一个正整数d，使得\(t=k_1d,n=k_2d\),又因为\(t=a*b[j]-k*n\),可以得到\(a*b[j]=k*k_2*d+k_d\),于是有\(a*b[j]\)和n存在一个大于1的公约数d，这与\(a*b[j]\)和n互质相矛盾，所以t与n也互质
对于\(a*b[1],a*b[2]\dots,a*b[\phi(n)]\),任意两个数模n的余数都不相同，也可以通过反证来证明。因此\(a*b[1],a*b[2]\dots,a*b[\phi(n)]\)模n的所有余数组成的集合，和\(b[1],b[2]\dots,b[\phi(n)]\)是相等的，所以有
\[b[1]b[2]\dots b[\phi(n)]\equiv a^{\phi(n)}b[1]b[2]\dots b[\phi(n)] \ \ (mod(n))\\
(a^{\phi(n)}-1)b[1]b[2]\dots b[\phi(n)]\equiv 0\\
a^{\phi(n)}\equiv1
\]
将如果n为质数的话，\(\phi(n)=n-1\),于是就有
\[a^{n-1}\equiv1\ \ mod(n) \ \text{n为质数}
\]
这实际上就是费马小定理
原根和阶
- 阶：在\(a\)和\(m\)互质的情况下，满足$a^x \equiv1 \(的最小的整数\)x\(,称作\)a\(关于\)m\(的阶，记作\)\delta_{m}(a)$
- 原根： 对\(a \in \Z\),满足\(\delta_{m}(a)=\varphi(m)\),则称\(a\)是\(m\)的一个原根
求阶
给定一个素数\(p\),回答T个询问，每次输入一个整数\(x\)，求\(\delta_{m}(x)\)
ll qmi(ll a,ll b,ll p){
ll res=1;
while(b){
if(b&1) res=res*a%p;
a=a*a%p;
b>>=1;
}
return res;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
int p,T;
cin>>p>>T;
int m=p-1;//p为质数，对应的欧拉函数就是p-1
//预处理数phi(m)的质因子
vector<int>pf;
for(int i=2;i<=m/i;i++){
if(m%i==0){
pf.push_back(i);
while(m%i==0) m/=i;
}
}
if(m!=1) pf.push_back(m);
for(int tc=1;tc<=T;tc++){
int x;
cin>>x;
int d=p-1;
//对每个质因子，按照能减就减的原则，求阶
for(auto u:pf){
while(d%u==0&&qmi(x,d/u,p)==1)
d/=u;
}
cout<<d<<endl;
}
}
原根
- 原根存在定理：一个数 \(m\) 存在原根，当且仅当 \(m=1,2,4,p^{\alpha},2p^{\alpha}\),其中\(p\)为奇素数，\(\alpha\)为正整数
- 若\(m\)存在原根，可以近似看作均匀分布，最小的原根\(g\)一定满足\(g\le m^{\frac{1}{4}} {}\)
- 若\(m\)存在原根，则原根的总个数为\(\varphi(\varphi(m))\)
-
最小原根的求法：
伪代码： 记m的欧拉函数为phi for i=1:m for m的所有质因子 u if i^{phi/u}=1 (mod m) i不满足条件 第一个满足条件的i，即为最小原根 -
求所有原根的方法
步骤： 1: 枚举和 \(\varphi(m)\) 互质的数\(t\)
2: 则 \(a^{t}\) 是一个原根
求解所有原根的时间复杂度\(O(log(n)\ n^{\frac{1}{4}}+\varphi(n))\)
洛谷 P6091
ll qmi(ll a,ll b,ll p){
ll res=1;
while(b){
if(b&1) res=res*a%p;
a=a*a%p;
b>>=1;
}
return res;
}
//得到一个数的欧拉函数
int get_phi(int n){
int m=n;
for(int i=2;i<=n/i;i++){
if(n%i==0){
m=m/i*(i-1);
while(n%i==0) n/=i;
}
}
if(n>1) m=m/n*(n-1);
return m;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
int T;
cin>>T;
while(T--){
int n,d;
cin>>n>>d;
int m=get_phi(n);
// cout<<"phi="<<m<<endl;
vector<int>p;
int x=m;
for(int i=2;i<=x/i;i++){
if(x%i==0){
p.push_back(i);
while(x%i==0) x/=i;
}
}
if(x>1) p.push_back(x);
//求最小原根
int mi=0;
for(int i=1;i<=n;i++){
if(gcd(i,n)!=1) continue;
bool flag=true;
for(auto u:p){
if(qmi(i,m/u,n)==1) {
flag=false;
break;
}
}
if(flag) {
mi=i;
break;
}
}
vector<int>res;
res.push_back(0);
if(mi){//用最小的原根去算其他原根
int tem=1;
for(int i=1;i<=m;i++){
tem=tem*mi%n;
if(gcd(i,m)!=1) continue;
res.push_back(tem);
}
}
sort(res.begin(),res.end());
cout<<res.size()-1<<endl;
for(int i=d;i<res.size();i+=d){
cout<<res[i]<<" ";
}
cout<<endl;
}
}
BSGS(指数方程)
给定\(p,a,b\)，其中\(p\)为质数(或者\(gcd(a,p)==1\)\(，求解最小的非负数\)x\(，使得\)\(x\)为满足条件$a^x\equiv b \mod p $的最小整数
引入分块的思想，另\(T=\lfloor \sqrt p \rfloor\),则\(x=qT-r ,其中1\le q,r\le T\),原方程等价于
\[a^x \equiv b \mod p\\
a^{qT-r}\equiv b \mod p\\
a^{qT}\equiv ba^r
\]
所以分别用一个hashtable记录左右两边分别枚举\(q\)和\(r\)所得的结果，看是否相等，并求最小的答案
- 洛谷 P3846
ll qmi(ll a,ll b,ll p){
ll res=1;
while(b){
if(b&1) res=res*a%p;
a=a*a%p;
b>>=1;
}
return res;
}
void solve(){
ll a,b,p;
cin>>p>>a>>b;
unordered_map<int,int>hs;
int T=sqrt(p)+2;
ll v=qmi(a,T,p),d=1;
for(int q=1;q<=T;q++){
d=d*v%p;
if(!hs.count(d)) hs[d]=q*T;
}
ll res=1e18;
d=b;
for(int r=1;r<=T;r++){
d=d*a%p;
if(hs[d]) res=min(res,1ll*hs[d]-r);
}
if(res==1e18) {
cout<<"no solution"<<endl;
}
else cout<<res<<endl;
}
扩展欧几里得算法
由裴蜀定理，可得
\[\forall x,y\in Z,f(x,y)=ax+by的最小正整数取值为gcd(a,b)
\]
\(x,y\) 一定可以取到
\[ax+by=gcd(a,b)=gcd(b,a\%b)=bx'+(a\%b)y'\\
=bx'+(a-[\frac{a}{b}]b)y'=ay'+b(x'-[\frac{a}{b}]y')\\
\text{所以有当x',y'已知时}\ \ x=y',y=x'-[\frac{a}{b}]y'
\]
我们可以递归的去求\(x'和y'\),递归中止条件\(b=0\),此时\((a,0)\)的最大公约数即为\(a\),可以令\(x=1,y=0\)
因为我们这里是递归求的，先求\(x'\)和\(y'\)的结果再得到\(x\)和\(y\),因此在传参的时候可以互换x和y的位置，这样里面一层递归结束后，\(x=y',y=x'\),于是只需要令\(y=y- [\frac{a}{b}]x\)
对于\(ax+by=d\)的所有解\(x,y\)，满足
\[x=x_0+kb/d\\
y=y_0-ka/d\\
\text{k为任意整数}，x_0和y_0为拓展欧几里得求出的解
\]
代码如下：
int exgcd(int a,int b,int &x,int &y){//一定要引用x和y
if(!b){
x=1,y=0;
return a;
}
int d=exgcd(b,a%b,y,x);
y-=a/b*x;
return d;//返回最大公约数
}
线性同余方程 acwing 878
要使得\(ax+by=c\)的\(x,y\)有整数解的充分必要条件是c是\((a,b)\)最大公约数的倍数
根据题意
\[ax\equiv b\ mod(m)\\
\Leftrightarrow (ax-b)\%m=0\\
\Leftrightarrow ax-b=-my\\
\Leftrightarrow ax+my=b\\
\]
所以
\[b\%gcd(a,m)\ne 0\text{ x无解}\\
b\%gcd(a,m)= 0\ \ \ x=x'[\frac{b}{gcd(a,b)}],\text{其中}x'为ax'+by'=gac(a,b)
\]
由于答案要在int范围内，所以对原式等价变形
\[ax+my=b\\
\Leftrightarrow a(km+r)+my=b\\
\Leftrightarrow ar+m(y+ak)=b\\
\text{所以令}\ x''=x\%m,y''=y+ak\text{等式结果不变}
\]
代码
#include<iostream>
using namespace std;
int exgcd(int a,int b,int &x,int &y)
{
if(!b){
x=1;
y=0;
return a;
}
int d=exgcd(b,a%b,y,x);
y-=a/b*x;
return d;
}
int main()
{
int n;
cin>>n;
while(n--)
{
int x,y,a,b,m;
scanf("%d%d%d",&a,&b,&m);
int r=exgcd(a,m,x,y);
if(b%r) cout<<"impossible"<<endl;
else cout<<(long long)x*b/r%m<<endl;
}
}
扩展欧几里得算法求逆元
对于\(x\times x^{-1} \equiv1\ \mod v\),其中\(x\)和\(v\)要满足互质，否则无解。快速幂求逆元只能解决\(v\)为质数的情况，当\(v\)不为质数的时候，由裴蜀定理,\(\exists \ m,n\in\ \Q\ \text{使得}\ m\times x+n\times v\equiv 1\) ，可以发现，这里的\(m\)其实就是x关于v的乘法逆元，对m取模即可
常用结论
-
对于两个互质的正整数\(p,q\),则\(px+qy\ (x>0,y>0)\)表示不出来的最大的数为\((p-1)(q-1)-1=qp-q-p\)
证明比较复杂，就不证了 -
对多个数的最大公约数，可以先求前两个数的最大公约数，利用这个公约数求下一个数与该数的最大公约数，即
\[(a,b,c,\dots i)=(gcd(a,b),c\dots,i)=(gcd(gcd(a,b),c)\dots i)\dots \]证明代证
中国剩余定理
对于\(x\in \Z\),有
\[\begin{cases}
x\equiv a_1\ \mod m_1\\
x\equiv a_2\ \mod m_2\\
\dots\\
x\equiv a_n\ \mod m_n
\end{cases}\
\\
\text{其中任意}m_i\text{互质}
\]
令
\[\begin{cases}
M=m_1m_2\dots m_n\\
M_i=\frac{M}{m_i}\\
t_i为M_i关于m_i的乘法逆元
\end{cases}
\]
则有
\[x=\sum_{i=1}^{n}a_iM_it_i \ \ \ \ mod\ M
\]
excrt 扩展中国剩余定理
当模数不互质的情况
-
牛客2023多校第一场L
#include<bits/stdc++.h> #define x first #define y second using namespace std; typedef long long LL; typedef pair<int,int> PII; typedef pair<LL,int> PLI; const int N=1e6+10,mod=998244353; int a[N],b[N],c[N]; int p[3][N],d[3][3][N],len[3][3],m[3],r[3]; void calc(int d[],int p[],int n,int st,int& len){ d[st]=0; int t=p[st],cnt=0; while(t!=st){ d[t]=++cnt; t=p[t]; } len=cnt+1; } LL exgcd(LL a,LL b,LL &x,LL &y) { if(!b) { x=1,y=0; return a; } int d=exgcd(b,a%b,y,x); y-=(LL)a/b*x; return d; } bool merge(LL &m1,LL&a1,LL m2,LL a2){ LL u,v; LL g=exgcd(m1,m2,u,v); LL m=m1/g*m2; if((a2-a1)%g) return false; LL d=(a2-a1)/g; LL x=(__int128(u)*m1*d+a1)%m; if(x<0) x+=m; m1=m,a1=x; return true; } LL excrt(int n){ LL b=m[0],a=r[0]; for(int j=1;j<n;j++) if(!merge(b,a,m[j],r[j])) return -1; LL res=(a%b+b)%b; return res; } int main(){ ios::sync_with_stdio(false); cin.tie(0),cout.tie(0); int n; cin>>n; for(int i=1;i<=n;i++) cin>>a[i]; for(int i=1;i<=n;i++) cin>>b[i]; for(int i=1;i<=n;i++) cin>>c[i]; memset(d,-1,sizeof d); for(int i=1;i<=n;i++) { p[0][i]=a[b[c[i]]]; p[1][i]=b[c[a[i]]]; p[2][i]=c[a[b[i]]]; } int x=1,y=1,z=1; for(int i=0;i<3;i++) { int x1,y1,z1; x1=a[y],y1=b[z],z1=c[x]; calc(d[i][0],p[0],n,x1,len[i][0]); calc(d[i][1],p[1],n,y1,len[i][1]); calc(d[i][2],p[2],n,z1,len[i][2]); x=x1,y=y1,z=z1; } int q; cin>>q; while(q--){ int ed[3]; LL ans=1e18; for(int i=0;i<3;i++) cin>>ed[i]; if(ed[0]==1&&ed[1]==1&&ed[2]==1) { cout<<0<<endl; continue; } for(int t=0;t<3;t++){ bool flag=true; for(int j=0;j<3;j++){ m[j]=len[t][j],r[j]=d[t][j][ed[j]]; if(r[j]==-1) flag=false; } if(!flag) continue; LL res=excrt(3); if(res!=-1) ans=min(ans,res*3+t+1); } if(ans==1e18) ans=-1; cout<<ans<<endl; } }
数论分块
- 引理1 对所有 \(\left \lfloor \frac{n}{i} \right \rfloor ,\ 1\le i\le n\text{中不同的数的个数}\le 2\sqrt n\)
- 引理2 对\(x\le n\),使得\(\left \lfloor\frac{n}{x}\right \rfloor=\left \lfloor\frac{n}{r}\right \rfloor,\ x\le r\le n\)的最大的整数\(r= \lfloor\frac{n}{ \lfloor \frac{n}{x}\rfloor} \rfloor\)
使用mobius函数和数论分块的一个例子 acwing 215
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N=5e4+10;
int prime[N],mobius[N],sum[N],cnt;
bool st[N];
void init(){
st[1]=true;
mobius[1]=1;
for(int i=2;i<N;i++){
if(!st[i]){
mobius[i]=-1;
prime[cnt++]=i;
}
for(int j=0;prime[j]*i<N;j++){
int t=prime[j]*i;
st[t]=true;
if(i%prime[j]==0){
mobius[t]=0;
break;
}
mobius[t]=mobius[i]*-1;
}
}
for(int i=1;i<N;i++) sum[i]=sum[i-1]+mobius[i];
}
int main()
{
int T;
cin>>T;
init();
while(T--){
int a,b,d;
cin>>a>>b>>d;
a/=d,b/=d;
int n=min(a,b);
LL res=0;
for(int l=1,r=1;l<=n;l=r+1){
r=min(n,min(a/(a/l),b/(b/l)));
res+=(LL)(sum[r]-sum[l-1])*(a/l)*(b/l);
}
cout<<res<<endl;
}
}
组合数
组合数求法
-
打表，根据公式
\[C_i^j=0\text{ if }j=0\\ C_i^j=C_{i-1}^j+C_{i-1}^{j-1}\text{ if }j\ne0\\ \]时间复杂度\(O(N^2)\),代码如下
#include<iostream> using namespace std; const int N=2010; const long long mod=1e9+7; int C[N][N]; void init() { C[0][0]=1; for(int i=1;i<N;i++) for(int j=0;j<N;j++) if(!j) C[i][j]=1; else C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod; } -
利用快速幂求组合数对一个质数取模后的结果
\[C_a^b=\frac{a!}{b!(a-b)!}\\ C_a^b\%p=(a!\%p\times(b!(a-b)!)^{-1}\%p)\%p\\ (b!(a-b)!)^{-1}\text{是 }b!(a-b)!\text{的逆元} \]因此只需要分别处理一遍\(fact(i)\mod p ,0\le i\le N\)的结果和利用快速幂处理\(infact[i]\ \mod p \ 0\le i\le N\)的结果
还有一点，乘法逆元满足如下性质：\[inv(a\times b)=inv(a)\times inv(b) \]所以
\[infact(b)=infact(b-1)\times inv(b) \]代码如下，时间复杂度\(O(Nlog_2(N))\)。
#include<iostream> using namespace std; typedef long long LL; int n; const int N=100010; int fact[N],infact[N]; const int mod=1e9+7; int qmi(int a,int b,int p){ int res=1; while(b){ if(b&1) res=(LL)res*a%p; b/=2; a=(LL)a*a%p; } return res; } int main() { int n; cin>>n; fact[0]=infact[0]=1; for(int i=1;i<N;i++){ fact[i]=(LL)fact[i-1]*i%mod; infact[i]=(LL)infact[i-1]*qmi(i,mod-2,mod)%mod; } for(int i=1;i<=n;i++) { int a,b; cin>>a>>b; LL res=(LL)fact[a]*infact[b]%mod*infact[a-b]%mod; cout<<res<<endl; } return 0; }
3.筛质数计算（高精度）
void init(int n){
for(int i=2;i<=n;i++)
{
if(!st[i]) prime[cnt++]=i;
for(int j=0;i*prime[j]<=n;j++)
{
st[i*prime[j]]=true;
if(i%prime[j]==0) break;
}
}
}
int get(int a,int p){
int res=0;
while(a){
res+=a/p;
a/=p;
}
return res;
}
vector<int> mul(vector<int> &A, int b) // C = A * b, A >= 0, b >= 0
{
vector<int> C;
int t=0;
for(int i=0;i<A.size()||t;i++){
if(i<A.size()) t+=A[i]*b;
C.push_back(t%10);
t/=10;
}
while(C.size()>1&&C.back()==0) C.pop_back();
return C;
}
vector<int> C(int n,int m){
vector<int> c;
c.push_back(1);
for(int i=0;i<cnt;i++){
int p=prime[i];
// cout<<p<<" ";
int s=get(n,p)-get(m,p)-get(n-m,p);
// cout<<s<<endl;
while(s--) c=mul(c,p);
}
return c;
}
void print(vector<int>&A){
while(A.size()&&A.back()==0) A.pop_back();
for(int i=A.size()-1;i>=0;i--)
printf("%d",A[i]);
}
Lucas定理
\[C_a^b=C_{a\%p}^{b\%p} \cdot C_{a/p}^{b/p} \mod p,\text{p为质数}
\]
代码 acwing1312
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 2e6+3,mod=1e6+3;
int fact[N],infact[N];
inline int qmi(int a,int b,int k){
int res=1;
while(b){
if(b&1) res=(LL)res*a%k;
a=(LL)a*a%k;
b>>=1;
}
return res;
}
inline void init(){
fact[0]=infact[0]=1;
for(int i=1;i<N;i++)
{
fact[i]=(LL)fact[i-1]*i%mod;
infact[i]=(LL)infact[i-1]*qmi(i,mod-2,mod)%mod;
}
}
inline int C(int a,int b){
return (LL)fact[a]*infact[b]%mod*infact[a-b]%mod;
}
inline int lucas(int a,int b){
if(a<mod&&b<mod) return C(a,b);
return (LL)C(a%mod,b%mod)*lucas(a/mod,b/mod)%mod;
}
int main()
{
int t;
cin>>t;
init();
while(t--){
int n,l,r;
cin>>n>>l>>r;
LL res=lucas(r-l+n+1,r-l+1)-1;
res=(res%mod+mod)%mod;
cout<<res<<endl;
}
return 0;
}
卡特兰数
卡特兰数为
\[H_n=C_{2n}^n-C^{n-1}_{2n}=\frac{C_{2n}^{n}}{n+1}
\]
可以理解为在在平面直角坐标系中，从(0,0)出发，每次只能向上走或者向右走，且不能越过\(y=x\)这条直线（可以碰到），之间求走到(n,n)的不同路径的数量
多项式
FFT快速傅里叶变换
位置换变换（蝴蝶变换
\(rev[i]\)：第 \(log(n)\) 层位置 \(i\) 上的数，对应的初始序列的下标
tot = 1 << bit;
for (int i = 0; i < tot; i++)
rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));
【模板】多项式乘法（FFT）
给定一个 \(n\) 次多项式 \(F(x)\)，和一个 \(m\) 次多项式 \(G(x)\)。
请求出 \(F(x)\) 和 \(G(x)\) 的卷积。
- 输入格式
第一行两个整数 \(n,m\)。
接下来一行 \(n+1\) 个数字，从低到高表示 \(F(x)\) 的系数。
接下来一行 \(m+1\) 个数字，从低到高表示 \(G(x)\) 的系数。
- 输出格式
一行 \(n+m+1\) 个数字，从低到高表示 \(F(x) \cdot G(x)\) 的系数。
对于 \(100\%\) 的数据：\(1 \le n, m \leq {10}^6\)。
核心代码
const double PI=acos(-1);
struct Complex //复数
{
double x, y;
Complex operator+(const Complex &t) const
{
return {x + t.x, y + t.y};
}
Complex operator-(const Complex &t) const
{
return {x - t.x, y - t.y};
}
Complex operator*(const Complex &t) const
{
return {x * t.x - y * t.y, x * t.y + y * t.x};
}
};
int rev[1<<24];
void init_fft(int bit){
int tot=1<<bit;
for(int i=0;i<tot;i++){
rev[i]=(rev[i>>1]>>1)|((i&1)<<(bit-1));
}
}
void fft(vector<Complex>&a, int inv,int tot)//inv为1表示fft,为-1表示ifft,逆变换后的系数还要除以tot
{
for (int i = 0; i < tot; i++)
{
if (i < rev[i])
swap(a[i], a[rev[i]]); //只需要交换一次就行了，交换两次等于没有换
}
for (int mid = 1; mid < tot; mid <<= 1)
{
auto w1 = Complex({cos(PI / mid), inv * sin(PI / mid)});
for (int i = 0; i < tot; i += mid * 2)
{
auto wk = Complex({1, 0}); //初始为w(0,mid),定义为w(k,mid)
for (int j = 0; j < mid; j++, wk = wk * w1) //单位根递推式
{
auto x = a[i + j], y = wk * a[i + j + mid];
a[i + j] = x + y, a[i + j + mid] = x - y;
}
}
}
}
vector<int> poly_mul(vector<int>&a,vector<int>&b,int sz){
int n=a.size(),m=b.size();
vector<int>res(sz);
int bit=0;
while((1<<bit)<=n+m+2) bit++;
init_fft(bit);
int tot=1<<bit;
vector<Complex>A(tot),B(tot);
for(int i=0;i<n;i++) A[i].x=a[i];
for(int i=0;i<m;i++) B[i].x=b[i];
fft(A,1,tot);
fft(B,1,tot);
for(int i=0;i<tot;i++)
A[i]=A[i]*B[i];
fft(A,-1,tot);
for(int i=0;i<sz;i++)
res[i]=(int)(A[i].x/tot+0.5);
return res;
}
洛谷 多项式乘法
#include <bits/stdc++.h>
using namespace std;
#define el '\n'
const int N = 4e6 + 10, M = 1e3 + 10;
const double PI = acos(-1);
int T, n, m;
struct Complex //复数
{
double x, y;
Complex operator+(const Complex &t) const
{
return {x + t.x, y + t.y};
}
Complex operator-(const Complex &t) const
{
return {x - t.x, y - t.y};
}
Complex operator*(const Complex &t) const
{
return {x * t.x - y * t.y, x * t.y + y * t.x};
}
} a[N], b[N];
int rev[N], bit, tot, res[N];
void fft(Complex a[], int inv)//inv为1表示fft,为-1表示ifft,逆变换后的系数还要除以tot
{
for (int i = 0; i < tot; i++)
{
if (i < rev[i])
swap(a[i], a[rev[i]]); //只需要交换一次就行了，交换两次等于没有换
}
for (int mid = 1; mid < tot; mid <<= 1)
{
auto w1 = Complex({cos(PI / mid), inv * sin(PI / mid)});
for (int i = 0; i < tot; i += mid * 2)
{
auto wk = Complex({1, 0}); //初始为w(0,mid),定义为w(k,mid)
for (int j = 0; j < mid; j++, wk = wk * w1) //单位根递推式
{
auto x = a[i + j], y = wk * a[i + j + mid];
a[i + j] = x + y, a[i + j + mid] = x - y;
}
}
}
}
void workFFT(int n, int m)
{// a[0, n], b[0, m]
while ((1 << bit) < n + m + 1)
bit++;
tot = 1 << bit;
for (int i = 0; i < tot; i++)
rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));
//递推(bit<<1)在bit之前，就已经被算出rev,最后一位是否为1
fft(a, 1), fft(b, 1);
for (int i = 0; i < tot; i++)
a[i] = a[i] * b[i]; //点表示法直接运算
fft(a, -1);//逆变换，点表示法转换为多项式表示法
//逆变换之后，
for (int i = 0; i <= n + m; i++)
res[i] = (int)(a[i].x / tot + 0.5); //向上去整
}
int main()
{
cin.tie(0);
cout.tie(0);
cin >> n >> m;
for (int i = 0; i <= n; i++)
cin >> a[i].x;
for (int i = 0; i <= m; i++)
cin >> b[i].x;
workFFT(n, m);
for (int i = 0; i <= n + m; i++)
cout << res[i] << ' ';
}
多项式全家桶
constexpr int P = 998244353;
using i64 = long long;
// assume -P <= x < 2P
int norm(int x) {
if (x < 0) {
x += P;
}
if (x >= P) {
x -= P;
}
return x;
}
template<class T>
T power(T a, int b) {
T res = 1;
for (; b; b /= 2, a *= a) {
if (b % 2) {
res *= a;
}
}
return res;
}
struct Z {
int x;
Z(int x = 0) : x(norm(x)) {}
int val() const {
return x;
}
Z operator-() const {
return Z(norm(P - x));
}
Z inv() const {
assert(x != 0);
return power(*this, P - 2);
}
Z &operator*=(const Z &rhs) {
x = i64(x) * rhs.x % P;
return *this;
}
Z &operator+=(const Z &rhs) {
x = norm(x + rhs.x);
return *this;
}
Z &operator-=(const Z &rhs) {
x = norm(x - rhs.x);
return *this;
}
Z &operator/=(const Z &rhs) {
return *this *= rhs.inv();
}
friend Z operator*(const Z &lhs, const Z &rhs) {
Z res = lhs;
res *= rhs;
return res;
}
friend Z operator+(const Z &lhs, const Z &rhs) {
Z res = lhs;
res += rhs;
return res;
}
friend Z operator-(const Z &lhs, const Z &rhs) {
Z res = lhs;
res -= rhs;
return res;
}
friend Z operator/(const Z &lhs, const Z &rhs) {
Z res = lhs;
res /= rhs;
return res;
}
friend std::istream &operator>>(std::istream &is, Z &a) {
i64 v;
is >> v;
a = Z(v);
return is;
}
friend std::ostream &operator<<(std::ostream &os, const Z &a) {
return os << a.val();
}
};
std::vector<int> rev;
std::vector<Z> roots{0, 1};
void dft(std::vector<Z> &a) {
int n = a.size();
if (int(rev.size()) != n) {
int k = __builtin_ctz(n) - 1;
rev.resize(n);
for (int i = 0; i < n; i++) {
rev[i] = rev[i >> 1] >> 1 | (i & 1) << k;
}
}
for (int i = 0; i < n; i++) {
if (rev[i] < i) {
std::swap(a[i], a[rev[i]]);
}
}
if (int(roots.size()) < n) {
int k = __builtin_ctz(roots.size());
roots.resize(n);
while ((1 << k) < n) {
Z e = power(Z(3), (P - 1) >> (k + 1));
for (int i = 1 << (k - 1); i < (1 << k); i++) {
roots[2 * i] = roots[i];
roots[2 * i + 1] = roots[i] * e;
}
k++;
}
}
for (int k = 1; k < n; k *= 2) {
for (int i = 0; i < n; i += 2 * k) {
for (int j = 0; j < k; j++) {
Z u = a[i + j];
Z v = a[i + j + k] * roots[k + j];
a[i + j] = u + v;
a[i + j + k] = u - v;
}
}
}
}
void idft(std::vector<Z> &a) {
int n = a.size();
std::reverse(a.begin() + 1, a.end());
dft(a);
Z inv = (1 - P) / n;
for (int i = 0; i < n; i++) {
a[i] *= inv;
}
}
struct Poly {
std::vector<Z> a;
Poly() {}
Poly(const std::vector<Z> &a) : a(a) {}
Poly(const std::initializer_list<Z> &a) : a(a) {}
int size() const {
return a.size();
}
void resize(int n) {
a.resize(n);
}
Z operator[](int idx) const {
if (idx < size()) {
return a[idx];
} else {
return 0;
}
}
Z &operator[](int idx) {
return a[idx];
}
Poly mulxk(int k) const {
auto b = a;
b.insert(b.begin(), k, 0);
return Poly(b);
}
Poly modxk(int k) const {
k = std::min(k, size());
return Poly(std::vector<Z>(a.begin(), a.begin() + k));
}
Poly divxk(int k) const {
if (size() <= k) {
return Poly();
}
return Poly(std::vector<Z>(a.begin() + k, a.end()));
}
friend Poly operator+(const Poly &a, const Poly &b) {
std::vector<Z> res(std::max(a.size(), b.size()));
for (int i = 0; i < int(res.size()); i++) {
res[i] = a[i] + b[i];
}
return Poly(res);
}
friend Poly operator-(const Poly &a, const Poly &b) {
std::vector<Z> res(std::max(a.size(), b.size()));
for (int i = 0; i < int(res.size()); i++) {
res[i] = a[i] - b[i];
}
return Poly(res);
}
friend Poly operator*(Poly a, Poly b) {
if (a.size() == 0 || b.size() == 0) {
return Poly();
}
int sz = 1, tot = a.size() + b.size() - 1;
while (sz < tot) {
sz *= 2;
}
a.a.resize(sz);
b.a.resize(sz);
dft(a.a);
dft(b.a);
for (int i = 0; i < sz; ++i) {
a.a[i] = a[i] * b[i];
}
idft(a.a);
a.resize(tot);
return a;
}
friend Poly operator*(Z a, Poly b) {
for (int i = 0; i < int(b.size()); i++) {
b[i] *= a;
}
return b;
}
friend Poly operator*(Poly a, Z b) {
for (int i = 0; i < int(a.size()); i++) {
a[i] *= b;
}
return a;
}
Poly &operator+=(Poly b) {
return (*this) = (*this) + b;
}
Poly &operator-=(Poly b) {
return (*this) = (*this) - b;
}
Poly &operator*=(Poly b) {
return (*this) = (*this) * b;
}
Poly deriv() const {
if (a.empty()) {
return Poly();
}
std::vector<Z> res(size() - 1);
for (int i = 0; i < size() - 1; ++i) {
res[i] = (i + 1) * a[i + 1];
}
return Poly(res);
}
Poly integr() const {
std::vector<Z> res(size() + 1);
for (int i = 0; i < size(); ++i) {
res[i + 1] = a[i] / (i + 1);
}
return Poly(res);
}
Poly inv(int m) const {
Poly x{a[0].inv()};
int k = 1;
while (k < m) {
k *= 2;
x = (x * (Poly{2} - modxk(k) * x)).modxk(k);
}
return x.modxk(m);
}
Poly log(int m) const {
return (deriv() * inv(m)).integr().modxk(m);
}
Poly exp(int m) const {
Poly x{1};
int k = 1;
while (k < m) {
k *= 2;
x = (x * (Poly{1} - x.log(k) + modxk(k))).modxk(k);
}
return x.modxk(m);
}
Poly pow(int k, int m) const {
int i = 0;
while (i < size() && a[i].val() == 0) {
i++;
}
if (i == size() || 1LL * i * k >= m) {
return Poly(std::vector<Z>(m));
}
Z v = a[i];
auto f = divxk(i) * v.inv();
return (f.log(m - i * k) * k).exp(m - i * k).mulxk(i * k) * power(v, k);
}
Poly sqrt(int m) const {
Poly x{1};
int k = 1;
while (k < m) {
k *= 2;
x = (x + (modxk(k) * x.inv(k)).modxk(k)) * ((P + 1) / 2);
}
return x.modxk(m);
}
Poly mulT(Poly b) const {
if (b.size() == 0) {
return Poly();
}
int n = b.size(); // eb + 1
std::reverse(b.a.begin(), b.a.end());
return ((*this) * b).divxk(n - 1); //保留系数(x ^ eb)及以上的
}
std::vector<Z> eval(std::vector<Z> x) const {
if (size() == 0) {
return std::vector<Z>(x.size(), 0);
}
const int n = std::max(int(x.size()), size());
std::vector<Poly> q(4 * n);
std::vector<Z> ans(x.size());
x.resize(n);
std::function<void(int, int, int)> build = [&](int p, int l, int r) {
if (r - l == 1) {
q[p] = Poly{1, -x[l]};
} else {
int m = (l + r) / 2;
build(2 * p, l, m);
build(2 * p + 1, m, r);
q[p] = q[2 * p] * q[2 * p + 1];
}
};
build(1, 0, n);
std::function<void(int, int, int, const Poly &)> work = [&](int p, int l, int r, const Poly &num) {
if (r - l == 1) {
if (l < int(ans.size())) {
ans[l] = num[0];
}
} else {
int m = (l + r) / 2;
work(2 * p, l, m, num.mulT(q[2 * p + 1]).modxk(m - l));
work(2 * p + 1, m, r, num.mulT(q[2 * p]).modxk(r - m));
}
};
work(1, 0, n, mulT(q[1].inv(n)));
return ans;
}
};
数据结构
哈希
模拟散列表
拉链法
#include <iostream>
#include <cstring>
#include <algorithm>
const int N = 1e5+3;//大于数据范围的第一个质数
using namespace std;
int h[N],e[N],ne[N],idx=0;
int insert(int x){
int k=(x%N+N)%N;
e[idx]=x;
ne[idx]=h[k];
h[k]=idx++;
}
bool find(int x){
int k=(x%N+N)%N;
for(int i=h[k];i!=-1;i=ne[i]){
if(e[i]==x) return true;
}
return false;
}
int main()
{
int n;
cin>>n;
char op[2];
int x;
memset(h, -1, sizeof h);
for(int i=1;i<=n;i++){
cin>>op>>x;
if(op[0]=='I') insert(x);
else if(find(x)) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}
}
开放寻址法
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 2e5+3,null=0x3f3f3f3f;//一般取数据范围的两倍
int h[N];
int find(int x){//如果x不在散列表中，则返回应该存放x的位置，否则返回x在散列表中的位置
int k=(x%N+N)%N;
while(h[k]!=null&&h[k]!=x)
{
k++;
if(k==N) k=0;
}
return k;
}
int main()
{
int n;
cin>>n;
char op[2];
int x;
memset(h,0x3f,sizeof h);
for(int i=1;i<=n;i++){
cin>>op>>x;
int k=find(x);
if(op[0]=='I') h[k]=x;
else {
if(h[k]!=null) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}
}
}
字符串哈希
acwing 841
对于一个字符串\(S\),可以把该字符串表示成一个p进制数，从右到左位数增加，即S的哈希值\(=\sum_{i=0}^{n-1}p^{n-i-1}S]i]\)
要求S字符串中从\([l,r]\)这一段的字符串的哈希值，需要将\([0,l-1]\)这一段字符串的哈希值左移\(r-l+1\)位，所以
这一段的哈希值=\(h[r]-h[l-1]*p[r-l+1]\)
代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int P=131;
const int N = 1e5+10;
typedef unsigned long long ULL;
char s[N];
ULL p[N],h[N];
ULL get(int l,int r){
return h[r]-h[l-1]*p[r-l+1];
}
int main()
{
int n,m;
cin>>n>>m;
cin>>s+1;
p[0]=1;
for(int i=1;i<=n;i++){
p[i]=p[i-1]*P;
h[i]=h[i-1]*P+s[i];
}
while(m--){
int l1,r1,l2,r2;
cin>>l1>>r1>>l2>>r2;
if(get(l1,r1)==get(l2,r2)) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}
}
单调栈
acwing 830 找到一组数字中每个数字左边第一个比它小的数字
代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N=1e5+10;
int ss[N],tt;
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++){
int x;
cin>>x;
while(tt&&ss[tt]>=x) tt--;
if(tt) cout<<ss[tt]<<" ";
else cout<<-1<<" ";
ss[++tt]=x;
}
}
树状数组
动态维护前缀和,单点修改和区间查询的时间复杂度都为\(O(log(n))\),区间修改可以转换成差分
\(tr[x]\)数组表示原数组从\((x-lowbit(x),x]\)的这一段的总和
int ans[N],h[N],tr[N];
int lowbit(int x){
return x&-x;
}
void add(int x,int c){
for(int i=x;i<=n;i+=lowbit(i)) tr[i]+=c;
}
int sum(int x){
int res=0;
for(int i=x;i;i-=lowbit(i)) res+=tr[i];
return res;
}
树状数组求前缀最大值
int lowbit(int x)
{
return x&-x;
}
void add(int x,LL c){
for(int i=x;i<=n;i+=lowbit(i)) tr[i]=max(tr[i],c);
}
LL query(int x){
LL res=0;
for(int i=x;i;i-=lowbit(i)) res=max(res,tr[i]);
return res;
}
线段树
按照一定属性维护一段区间，通常开4N大小,tr[4N]是一个结构体，包含要维护的性质，从1开始编号，表示一整段区间的性质
对于编号u，\(左边区间编号u<<1,右边区间编号u<<1|1\)
单点修改的线段树
- acwing 245. 你能回答这些问题吗
给定一个数组，有单点修改和查询区间最大子段和
#include<bits/stdc++.h>
#define x first
#define y second
using namespace std;
typedef long long ll;
typedef long long i64;
typedef pair<int, int> PII;
typedef pair<ll, ll> Pll;
const double PI=acos(-1);
const int N=5e5+10,INF=2e9;
struct info{
ll mss,pres,sufs,s;//区间最大字段和，最大前缀和，最大后缀和，和
info(int a=-INF):mss(a),pres(a),sufs(a),s(a){}
};
info operator+(const info& l,const info& r){
info a;
a.mss=max({l.mss,r.mss,l.sufs+r.pres});
a.pres=max(l.pres,l.s+r.pres);
a.sufs=max(r.sufs,l.sufs+r.s);
a.s=l.s+r.s;
return a;
}
struct node{
int l,r;
info val;//记录信息
}tr[4*N];
int a[N];
void pushup(int u){
tr[u].val=tr[u<<1].val+tr[u<<1|1].val;
}
void build(int u,int l,int r){
if(l==r) tr[u]={l,r,info(a[l])};
else {
tr[u]={l,r};
int mid=l+r>>1;
build(u<<1,l,mid),build(u<<1|1,mid+1,r);
pushup(u);
}
}
void change(int u,int pos,int val){
if(tr[u].l==tr[u].r){
tr[u].val=info(val);
}
else {
int mid=tr[u].l+tr[u].r>>1;
if(pos>mid) change(u<<1|1,pos,val);
else change(u<<1,pos,val);
pushup(u);
}
}
info query(int u,int l,int r){
if(tr[u].l>=l&&tr[u].r<=r){
return tr[u].val;
}
else {
int mid=tr[u].l+tr[u].r>>1;
if(l>mid) return query(u<<1|1,l,r);
else if(r<=mid) return query(u<<1,l,r);
else return query(u<<1,l,r)+query(u<<1|1,l,r);
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i];
build(1,1,n);
while(m--){
int op,l,r;
cin>>op>>l>>r;
if(op==1) {
if(l>r) swap(l,r);
auto t=query(1,l,r);
cout<<t.mss<<endl;
}
else change(1,l,r);
}
}
区间修改的线段树
- acwing 1277. 维护序列
给定一个数列，有如下三种操作形式：
- 把数列中的一段数全部乘一个值；
- 把数列中的一段数全部加一个值；
- 询问数列中的一段数的和模上\(mod\)的值
#include<bits/stdc++.h>
#define x first
#define y second
using namespace std;
typedef long long ll;
const int N=1e5+10,INF=2e9;
int mod;
struct tag{
ll mul,add;
tag(ll m=1,ll a=0):mul(m),add(a){}
};
tag operator+(const tag& l,const tag& r){//两个tag相加
return {l.mul*r.mul%mod,(l.add*r.mul+r.add)%mod};
}
struct node{
int l,r;
ll val;
tag t;
}tr[4*N];
void settag(int u,tag t){//给一段区间加上tag
tr[u].t=tr[u].t+t;
tr[u].val=(tr[u].val*t.mul+t.add*(tr[u].r-tr[u].l+1))%mod;
}
int a[N];
void pushup(int u){
tr[u].val=(tr[u<<1].val+tr[u<<1|1].val)%mod;
}
void pushdown(int u){
if(tr[u].t.mul!=1||tr[u].t.add!=0){
settag(u<<1,tr[u].t);
settag(u<<1|1,tr[u].t);
tr[u].t={1,0};
}
}
void build(int u,int l,int r){
if(l==r) tr[u]={l,r,a[l]};
else {
tr[u]={l,r};
int mid=l+r>>1;
build(u<<1,l,mid),build(u<<1|1,mid+1,r);
pushup(u);
}
}
void modify(int u,int l,int r, tag t){
if(tr[u].l>=l&&tr[u].r<=r){
settag(u,t);
}
else {
pushdown(u);
int mid=tr[u].l+tr[u].r>>1;
if(l<=mid) modify(u<<1,l,r,t);
if(r>mid) modify(u<<1|1,l,r,t);
pushup(u);
}
}
ll query(int u,int l,int r){
if(tr[u].l>=l&&tr[u].r<=r){
return tr[u].val;
}
else {
pushdown(u);
int mid=tr[u].l+tr[u].r>>1;
if(l>mid) return query(u<<1|1,l,r);
else if(r<=mid) return query(u<<1,l,r);
else return (query(u<<1,l,r)+query(u<<1|1,l,r))%mod;
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
int n,m;
cin>>n>>mod;
for(int i=1;i<=n;i++) cin>>a[i];
build(1,1,n);
cin>>m;
while(m--){
int op,l,r,c;
cin>>op>>l>>r;
if(op==1){
cin>>c;
modify(1,l,r,{c,0});
}
else if(op==2){
cin>>c;
modify(1,l,r,{1,c});
}
else {
cout<<query(1,l,r)<<endl;
}
}
}
可持久化数据结构
可持久化线段树（主席树）
可持久化数组
#include <iostream>
#include <cstring>
#include <algorithm>
#include<vector>
#include<queue>
#include<set>
#include<unordered_map>
#include<cmath>
#include<map>
#include<unordered_set>
#define x first
#define y second
using namespace std;
typedef pair<int,int> PII;
typedef long long LL;
const int N=1e6+10;
struct node{
int l,r;
int v;
}tr[N*4+N*20];
int root[N],idx;
int a[N];
int build(int l,int r){
int p=++idx;
if(l==r) tr[p].v=a[l];
else{
int mid=l+r>>1;
tr[p].l=build(l,mid);
tr[p].r=build(mid+1,r);
}
return p;
}
int update(int p,int l,int r,int k,int v){
int q=++idx;
tr[q]=tr[p];
if(l==r) tr[q].v=v;
else{
int mid=l+r>>1;
if(k<=mid) tr[q].l=update(tr[q].l,l,mid,k,v);
else tr[q].r=update(tr[q].r,mid+1,r,k,v);
}
return q;
}
int query(int p,int l,int r,int k){
if(l==r) return tr[p].v;
int mid=l+r>>1;
if(k<=mid) return query(tr[p].l,l,mid,k);
else return query(tr[p].r,mid+1,r,k);
}
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
root[0]=build(1,n);
for(int i=1;i<=m;i++){
int vi,op,loc,val;
scanf("%d%d%d",&vi,&op,&loc);
if(op==1){
scanf("%d",&val);
root[i]=update(root[vi],1,n,loc,val);
}
else
{
root[i]=root[vi];
cout<<query(root[vi],1,n,loc)<<endl;
}
}
}
离线分治
返回m个区间内第k小的数
#include <iostream>
#include <cstring>
#include <algorithm>
#define lc(x) tr[x].l
#define rc(x) tr[x].r
using namespace std;
vector<int> v;
const int N = 1e5+10;
struct node{
int l,r;
int cnt;
}tr[N*22];
int root[N],idx;
vector<int>nums;
int a[N];
int find(int x){
return lower_bound(nums.begin(),nums.end(),x)-nums.begin();
}
int build(int l,int r){
int p=++idx;
if(l==r) return p;
int mid=l+r>>1;
tr[p].l=build(l,mid),tr[p].r=build(mid+1,r);
return p;
}
int insert(int pre,int l,int r,int x){
int q=++idx;
tr[q]=tr[pre];
tr[q].cnt++;
if(l==r) return q;
int mid=l+r>>1;
if(x<=mid) lc(q)=insert(lc(q),l,mid,x);
else rc(q)=insert(rc(q),mid+1,r,x);
return q;
}
int query(int x,int y,int l,int r,int k){
if(l==r) return l;
int mid=l+r>>1;
int sum=tr[tr[y].l].cnt-tr[tr[x].l].cnt;
if(k<=sum) return query(lc(x),lc(y),l,mid,k);
else return query(rc(x),rc(y),mid+1,r,k-sum);
}
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
nums.push_back(a[i]);
}
sort(nums.begin(),nums.end());
nums.erase(unique(nums.begin(),nums.end()),nums.end());
root[0]=build(0,nums.size()-1);
for(int i=1;i<=n;i++)
root[i]=insert(root[i-1],0,nums.size()-1,find(a[i]));
while(m--){
int l,r,k;
cin>>l>>r>>k;
cout<<nums[query(root[l-1],root[r],0,nums.size()-1,k)]<<endl;
}
return 0;
}
ST表
利用倍增的思想，当要求查询一段区间上符合结合律且可重复贡献的信息查询时（如最大值，最小值，最大公约数，最小公倍数），对原数据预处理
以最大值为例，\(f[i][j]\)表示在\(i,i+2^j-1\)这段区间上的最大值，于是有递推式
\[f[i][j]=max(f[i][j-1],f[i+2^{j-1}][j-1])
\]
预处理
int f[MAXN][21]; // 第二维的大小根据数据范围决定，不小于log(MAXN)
for (int i = 1; i <= n; ++i)
f[i][0] = read(); // 读入数据
for (int i = 1; i <= 20; ++i)
for (int j = 1; j + (1 << i) - 1 <= n; ++j)
f[j][i] = max(f[j][i - 1], f[j + (1 << (i - 1))][i - 1]);
对于一段给定的区间\([l,r]\),想访问这段区间的最大值，可以令$s=\left \lfloor log_2(r-l+1) \right \rfloor \(,最大值一定在\)[l,l+2s-1]$和$[r-2s+1,r]$这两段子区间内取到
查询
while(q--)
{
int l,r;
cin>>l>>r;
int s=Log2[r-l+1];
int a=max(f[l][s],f[r-(1<<s)+1][s]);
cout<<a<<endl;
}
也可以预处理一下\(log_2[x]\)数组
for(int i=2;i<=n;i++)
Log2[i]=Log2[i/2]+1;
整体的时间复杂度为\(O(nlog_2n)\)
除了查询区间的某一个属性，st表还可以利用倍增的思想解决类似于找到某一个点左边第一个比它大（小）的数所在的位置。
莫队
离线莫队
给定给出一个长度为n 的数列，有q 个询问，每个询问给出数对\((i,j)\)，需要你给出\(a_i,a_{i+1},…… a_j\) ，这一段中有多少不同的数字
时间复杂度\(O(n\sqrt q)\)
const int N =3e6 + 10, mod = 998244353, B = 600;
int cnt[N],num[N];
void solve()
{
int n,q,ans=0;
cin>>n;
for(int i=1;i<=n;i++) cin>>num[i];
cin>>q;
vector<array<int,3>>seg(q);
vector<int>res(q);
for(int i=0;i<q;i++){
int l,r;
cin>>l>>r;
seg[i]={l,r,i};
}
sort(seg.begin(),seg.end(),[&](array<int,3> a,array<int,3> b){
if(a[0]/B!=b[0]/B) return a[0]/B<b[0]/B;
else return a[1]>b[1];
});
int l=1,r=0;
auto add=[&](int x){
if(!cnt[num[x]]) ans++;
cnt[num[x]]++;
};
auto del=[&](int x){
if(cnt[num[x]]==1) ans--;
cnt[num[x]]--;
};
for(int i=0;i<q;i++){
while(r<seg[i][1]) add(++r);
while(l<seg[i][0]) del(l++);
while(r>seg[i][1]) del(r--);
while(l>seg[i][0]) add(--l);
res[seg[i][2]]=ans;
}
for(int i=0;i<q;i++)
cout<<res[i]<<endl;
}
2023牛客多校5 A
#include <iostream>
#include <cassert>
#include <cstring>
#include <string>
#include <map>
#include <cmath>
#include <vector>
#include <queue>
#include <algorithm>
#include <unordered_map>
#include <set>
#include <map>
#include <stack>
#include <functional>
#include <fstream>
#include <sstream>
#include <bitset>
#include <numeric>
#include <iomanip>
#define x first
#define y second
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
typedef pair<LL, int> PLI;
const int N =5e5+10, mod = 998244353;
int cnt[N];
LL sum[N];
int a[N],tr[N],b[N],n,m;
int lowbit(int x){
return x&-x;
}
void add(int x,int c){
for(int i=x;i<=n;i+=lowbit(i)) tr[i]+=c;
}
int query(int u){
int res=0;
for(int i=u;i;i-=lowbit(i)) res+=tr[i];
return res;
}
void solve()
{
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i];
vector<array<int,3>>seg(m);
vector<LL>ans(m);
int B=sqrt(n)+1;
for(int i=0;i<m;i++){
int l,r;
cin>>l>>r;
seg[i]={l,r,i};
}
sort(seg.begin(),seg.end(),[&](array<int,3>x,array<int,3>y){
if(x[0]/B!=y[0]/B) return x[0]<y[0];
return (x[0]/B&1)?x[1]<y[1]:x[1]>y[1];
});
for(int i=1;i<=n;i++) b[i]=query(a[i]-1),add(a[i],1);
int l=1,r=0;
LL res=0;
auto addL= [&](int x){
res+=sum[a[x]]-(LL)cnt[a[x]]*b[x];
sum[a[x]]+=b[x],cnt[a[x]]++;
};
auto addR= [&](int x){
res+=(LL)cnt[a[x]]*b[x]-sum[a[x]];
sum[a[x]]+=b[x],cnt[a[x]]++;
};
auto delL=[&](int x){
sum[a[x]]-=b[x],cnt[a[x]]--;
res-=sum[a[x]]-(LL)cnt[a[x]]*b[x];
};
auto delR=[&](int x){
sum[a[x]]-=b[x],cnt[a[x]]--;
res-=(LL)cnt[a[x]]*b[x]-sum[a[x]];
};
for(int i=0;i<m;i++){
while(r<seg[i][1]) addR(++r);
while(r>seg[i][1]) delR(r--);
while(l<seg[i][0]) delL(l++);
while(l>seg[i][0]) addL(--l);
ans[seg[i][2]]=res;
}
for(int i=0;i<m;i++)
cout<<ans[i]<<"\n";
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
int T = 1;
while (T--)
solve();
}
dsu on tree
本质上还是启发式合并，不过有更小的常数
大致的思路是：
-
给每个节点，记录一下节点数最多的一个儿子，称作重儿子，其他的儿子称作轻儿子
-
对轻儿子，合并到重儿子的集合中，父节点也合并到重儿子的集合中，这样一直在维护一个集合
-
通过add，del操作，维护重儿子的信息，而轻儿子，在合并后清空信息
这样每个节点最多被合并\(log(n)\) 次，总的时间复杂度\(O(nlog(n))\),空间复杂度\(O(n)\)
CF 600E
给定一棵树，每个节点有一个颜色，求每个子树颜色众数的颜色编号和
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+10;
vector<int>e[N];
int l[N],r[N],sz[N],hs[N],id[N],tot;
int c[N],cnt[N];
ll ans[N],sumcnt,maxcnt;
void dfs_init(int u,int fa){//初始化dfs序
l[u]=++tot;
id[tot]=u;
sz[u]=1;
hs[u]=-1;
for(auto v:e[u]){
if(v==fa) continue;
dfs_init(v,u);
sz[u]+=sz[v];
if(~hs[u]||sz[v]>sz[hs[u]])//找到节点最多的子树
hs[u]=v;
}
r[u]=tot;
}
void dfs_solve(int u,int fa,bool keep){
for(auto v:e[u]){//递归解决轻儿子
if(v!=fa&&v!=hs[u])
dfs_solve(v,u,false);
}
if(hs[u]!=-1){//递归解决重儿子
dfs_solve(hs[u],u,true);
}
auto add=[&](int x){
x=c[x];
cnt[x]++;
if(cnt[x]>maxcnt) maxcnt=cnt[x],sumcnt=0;
if(cnt[x]==maxcnt) sumcnt+=x;
};
auto del=[&](int x){
x=c[x];
cnt[x]--;
};
for(auto v:e[u]){//合并轻儿子到重儿子上
if(v!=fa&&v!=hs[u])
for(int i=l[v];i<=r[v];i++)
add(id[i]);
}
add(u);//加入自自身
ans[u]=sumcnt;
if(!keep){//如果是轻儿子，清空子树
maxcnt=sumcnt=0;
for(int i=l[u];i<=r[u];i++)
del(id[i]);
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
int n;
cin>>n;
for(int i=1;i<=n;i++) cin>>c[i];
for(int i=1;i<n;i++){
int u,v;
cin>>u>>v;
e[u].push_back(v);
e[v].push_back(u);
}
dfs_init(1,0);
dfs_solve(1,0,false);
for(int i=1;i<=n;i++)
cout<<ans[i]<<" ";
}
字符串
KMP
\(s\)为主串，\(p\)为模式串，最后输出答案下标从0开始
#include<iostream>
using namespace std;
const int N=100010,M=1000010;
char s[M],p[N];
int ne[N];
int main()
{
int n,m;
cin>>n>>p+1>>m>>s+1;
for(int i=2,j=0;i<=n;i++)
{
while(j&&p[i]!=p[j+1]) j=ne[j];
if(p[j+1]==p[i]) j++;
ne[i]=j;
}
for(int i=1,j=0;i<=m;i++)
{
while(j&&s[i]!=p[j+1]) j=ne[j];
if(s[i]==p[j+1]) j++;
if(j==n) {
cout<<i-n<<" ";
j=ne[j];
};
}
}
Trie树
acwing 143 最大异或对
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e5*32+10;
int son[N][2];
int idx=0;
void insert(int x){
int p=0;
for(int i=30;i>=0;i--){
int u=x>>i&1;
if(!son[p][u]) son[p][u]=++idx;
p=son[p][u];
}
}
int search(int x){
int p=0;
int res=0;
for(int i=30;i>=0;i--){
int u=x>>i&1;
if(son[p][!u]) {
res=res*2+!u;
p=son[p][!u];
}
else {
res=res*2+u;
p=son[p][u];
}
}
return res;
}
int main()
{
int n;
cin>>n;
int ans=0;
while(n--){
int x;
scanf("%d",&x);
insert(x);
ans=max(ans,x^search(x));
}
cout<<ans;
}
manacher
\(O(n)\)的时间复杂度内求出最大回文长度
const int N=1.1e7+10;
char s[N],t[2*N];
int p[N*2];
int manacher(){
int n=strlen(s+1);
int m=0;
t[++m]='$';
for(int i=1;i<=n;i++)
t[++m]=s[i],t[++m]='$';//预处理使得原始串变成奇数长度
int M=0,R=0;
for(int i=1;i<=m;i++){
if(i>R) p[i]=1;
else p[i]=min(p[2*M-i],R-i+1);//i关于M的对称点k=2*M-1，若k-p[k]>L,则p[i]=p[k],否则还要暴力扩展
while(i+p[i]<=m&&i-p[i]>=1&&t[i+p[i]]==t[i-p[i]])//向左右两边扩展
++p[i];
if(i+p[i]-1>R) M=i,R=i+p[i]-1;
}
int ans=0;
for(int i=1;i<=m;i++) ans=max(ans,p[i]);
return ans-1;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
scanf("%s",s+1);
cout<<manacher()<<endl;
}
最小表示法
在\(O(n)\)的时间复杂度内，求出一个字符串的循环同构中的字典序最小的表示
string get_min(string a){
int n=a.size();
a='#'+a;
for(int i=1;i<=n;i++)
a.push_back(a[i]);
int i=1,j=2;
while(j<=n){
int k=0;
while(k<n&&a[i+k]==a[j+k]) k++;
if(a[i+k]>a[j+k]) i+=k+1;
else j+=k+1;
if(i==j) j++;
if(i>j) swap(i,j);
}
string res;
for(int t=i;t<i+n;t++)
res+=a[t];
return res;
}
搜索
DFS 剪枝
acwing 168 生日蛋糕
7 月 17 日是 Mr.W 的生日，ACM-THU 为此要制作一个体积为 Nπ 的 M 层生日蛋糕，每层都是一个圆柱体。
设从下往上数第 i 层蛋糕是半径为 Ri，高度为 Hi 的圆柱。
当 i<M 时，要求 Ri>Ri+1 且 Hi>Hi+1。
由于要在蛋糕上抹奶油，为尽可能节约经费，我们希望蛋糕外表面（最下一层的下底面除外）的面积 Q 最小。
令 Q=Sπ ，请编程对给出的 N 和 M，找出蛋糕的制作方案（适当的 Ri 和 Hi 的值），使 S 最小。
除 Q 外，以上所有数据皆为正整数。
输入格式
输入包含两行，第一行为整数 N，表示待制作的蛋糕的体积为 Nπ。
第二行为整数 M，表示蛋糕的层数为 M。
输出格式
输出仅一行，是一个正整数 S（若无解则 S=0）。
数据范围
1≤N≤10000,
1≤M≤20
输入样例：
100
2
输出样例：
68
dfs 剪枝操作
- 自底向上搜，减少分支数
- 枚举的时候，先枚举R,再枚举h
- 从上到下，对第u层，有
\(u\le R_u\le min(R_{u+1}-1,\sqrt{n-v})\)
\(u\le H_u\le min(H_{u+1}-1,\frac{n-v}{R^2})\) - 对于预处理的minv, minu有
\(V+minv(u)\le n\)
\(S+mins(u)\le ans\),其中V和S是当前已经计算的从第m层到第u-1层的总体积和总面积 最重要的一步
\(S+\frac{2(n-v)}{R_{u+1}}\ge ans\) 时，剪枝
证明：
\(S_{1\sim u}=\sum_{k=1}^u 2R_kH_k\)
\(V_{1\sim u}=n-v=\sum_{k=1}^u R_k^2H_k\)
\(\because S_{1\sim u}=\frac{2}{R_{u+1}}\sum_{k=1}^u R_kH_kR_{u+1}\ge \frac{2(n-v)}{R_{u+1}}\)
\(\therefore 当S+\frac{2(n-v)}{R_{u+1}}\ge ans\)
有\(S+S_{1\sim u}=S_总\ge ans\)
C++代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <cmath>
#include<unordered_map>
#define x first
#define y second
using namespace std;
const int M=25;
int n,m,res=0x3f3f3f3f;
int minv[M],mins[M],R[M],H[M];
void dfs(int u,int v,int s)
{
if(v+minv[u]>n) return ;
if(s+mins[u]>=res) return;
if(s+2*(n-v)/R[u+1]>=res) return;
if(!u)
{
if(v==n)
res=s;
return ;
}
for(int r=min(R[u+1]-1,(int)sqrt(n-v));r>=u;r--)
for(int h=min(H[u+1]-1,(n-v)/r/r);h>=u;h--)
{
int t=0;
if(u==m) t=r*r;
R[u]=r,H[u]=h;
dfs(u-1,v+r*r*h,s+t+2*r*h);
}
}
int main()
{
cin>>n>>m;
for(int i=1;i<=m;i++)
{
minv[i]=minv[i-1]+i*i*i;
mins[i]=mins[i-1]+2*i*i;
}
R[m+1]=H[m+1]=0x3f3f3f3f;
dfs(m,0,0);
if(res==0x3f3f3f3f) res=0;
cout<<res<<endl;
}
图论
单源最短路
Dijkstra算法
利用贪心策略，用一个已经确定最短距离的点的集合S，每次找到距离集合S距离最近的一个点，将其加入到S中，利用该点更新起点距离其他点的最短距离。一旦把一个点放入集合中，其最短距离就已经确定了，可以用反证法证明
假设当前被加入到集合S的点A会被集合S外的另一个点B更新，那么就有\(dist[B]+w_{ba}\le dist[A]\)就有\(dist[B]<dist[A]\),与A是距离集合最近的一点矛盾
朴素版
时间复杂度\(O(n^2)\)
int g[N][N];
int n,m;
int d[N];
bool st[N];
int dijkstra()
{
memset(d,0x3f,sizeof d);
d[1]=0;//从第一个点开始
for(int i=1;i<n;i++)
{
int t=-1;
for(int j=1;j<=n;j++)
if(!st[j]&&(t==-1||d[t]>d[j]))
t=j;
for(int j=1;j<=n;j++)
d[j]=min(d[t]+g[t][j],d[j]);
st[t]=true;
}
if(d[n]==INF) return -1;
else return d[n];
}
堆优化版
时间复杂度\(O(mlog(n))\)
typedef pair<int, int> PII;
const int N = 1e6 + 10;
int n, m;
int h[N], w[N], e[N], ne[N], idx;
int dist[N];
bool st[N];
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
int dijkstra()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
priority_queue<PII, vector<PII>, greater<PII>> heap;
heap.push({0, 1});
while (heap.size())
{
auto t = heap.top();
heap.pop();
int ver = t.second, distance = t.first;
if (st[ver]) continue;//同一个点可能会被加入堆多次，只有第一次更新是有用的
st[ver] = true;
for (int i = h[ver]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[ver] + w[i])
{
dist[j] = dist[ver] + w[i];
heap.push({dist[j], j});
}
}
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
bellman-ford
Bellman - ford 算法是求含负权图的单源最短路径的一种算法，效率较低，代码难度较小。其原理为连续进行松弛，在每次松弛时把每条边都更新一下，若在 n-1 次松弛后还能更新，则说明图中有负环，因此无法得出结果，否则就完成。
时间复杂度\(O(nm)\),可以处理带有负权回路的情况
#include<iostream>
#include<cstring>
using namespace std;
const int N=510,M=10010;
int n,m,k;
bool st[N];
int back[N];
int dist[N];
struct {
int a,b,w;
}edge[M];
void bellman_ford()
{
memset(dist,0x3f,sizeof dist);
dist[1]=0;
for(int i=0;i<k;i++)
{
memcpy(back,dist,sizeof dist);//要用经过1~i-1的状态跟新第i层
for(int j=0;j<m;j++)
{
auto e=edge[j];
if(dist[e.b]>back[e.a]+e.w) dist[e.b]=back[e.a]+e.w;
}
}
}
int main()
{
cin>>n>>m>>k;
for(int i=0;i<m;i++)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
edge[i]={a,b,c};
}
bellman_ford();
if(dist[n]>0x3f3f3f3f/2) cout<<"impossible"<<endl;
else cout<<dist[n]<<endl;
}
spfa
对bellman-ford的一种优化，每次只对队头去除的点周围的边进行松弛操作，时间复杂度最坏在\(O(nm)\),一般情况下为\(kO(n)\),k为常数
int dist[N];
bool st[N];
int spfa()
{
memset(dist,0x3f,sizeof dist);
memset(st,0,sizeof st);
dist[0]=0;
queue<int>q;
q.push(0);
while(q.size())
{
auto t=q.front();
q.pop();
st[t]=false;
for(int i=h[t];i!=-1;i=ne[i])
{
int j=e[i];
if(dist[j]>dist[t]+w[i])
{
dist[j]=dist[t]+w[i];
if(!st[j])
{
st[j]=true;
q.push(j);
}
}
}
}
if(dist[s]==INF) return -1;
else return dist[s];
}
多源最短路
Floyd算法
- 原理
Floyd可以看作是一种dp,初始化\(dist[i][j]=\begin{cases} INF&\ i\ne j\\0& i=j\end{cases}\)，令\(dist[k][i][j]\)表示，从i到j经过前k个点的最短距离
状态转移方程\(dist[k][i][j]=min(dist[k-1][i][j],dist[k-1][i][k]+dist[k-1][k][j])\)
只用到了第k-1层的状态，所以可以优化为\(dist[i][j]=min(dist[i][j],dist[i][k]+dist[k][j])\),(i或j等于k时，\(dist[k][k]=0\)，相当于没有更新)
最基本的代码
void floyd()
{
memset(g,0x3f,sizeof g);
for(int i=1;i<=n;i++) g[i][i]=0;
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
g[i][j]=min(g[i][j],g[i][k]+g[k][j]);
}
Floyd的拓展
- 传递闭包
- 找最小环
- 恰好经过k条边的最短路(倍增)
最小生成树
prim算法
同dijkstra很类似，prim也是一种基于贪心的做法，从起点开始，每次找到距离当前选中的集合最近的一个点，将其加入到集合中，不断重复n次，可以得到最优解
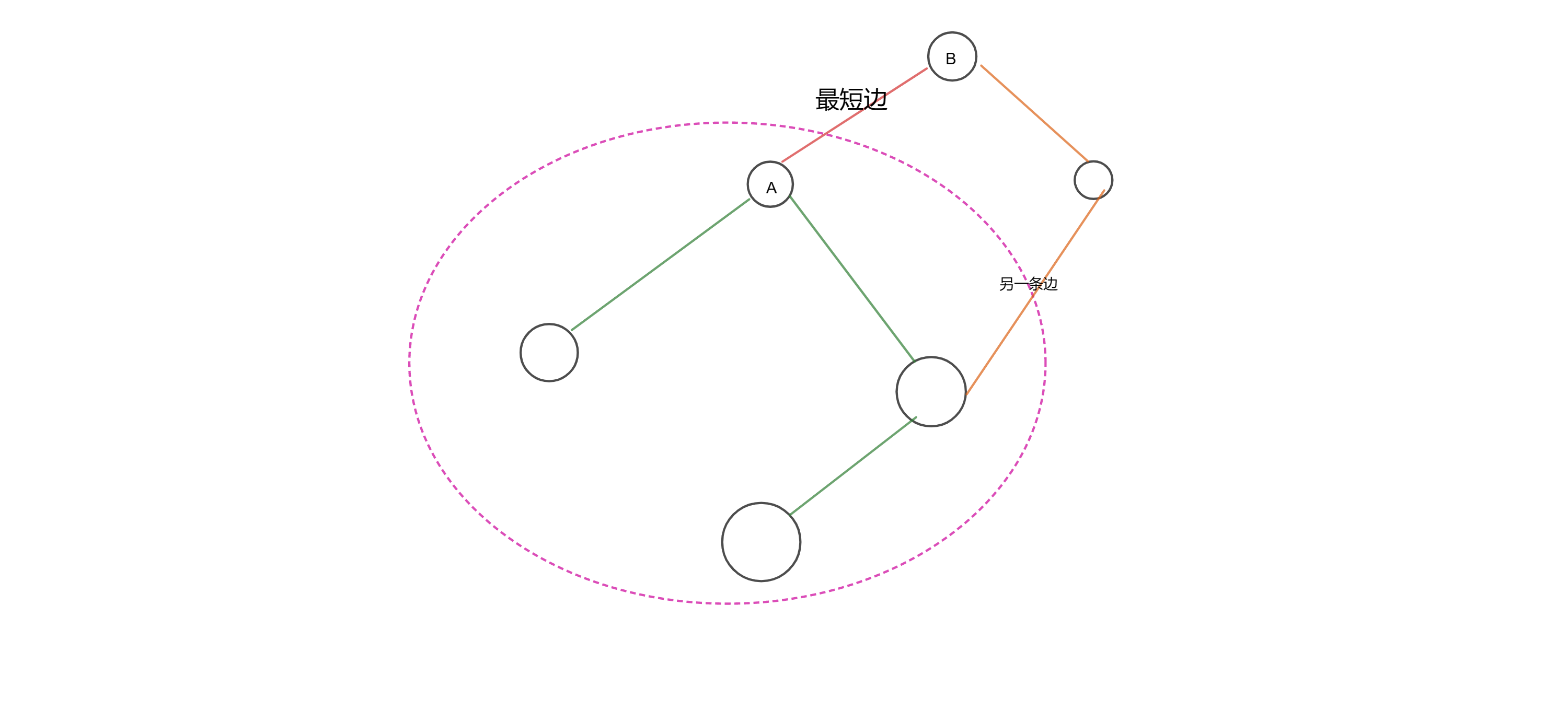
证明 当前距离集合最近的一个点是B,那么假设存在一条不经过AB边的路径，使得A与B两点联通，此时加上AB边一定会构成一条从A到B的回路，而我们选择的另一条边权值一定大于最短边，所以可以用AB替换选择的另一条边，连通性不变而生成树的权值减小，与假设矛盾，所以应当选择距离集合最近的一条边
int n, dist[N];
int g[N][N];
bool st[N];
int prim()
{
memset(dist,0x3f,sizeof dist);
dist[1]=0;
int res=0;
for(int i=0;i<n;i++)
{
int t=-1;
for(int j=1;j<=n;j++)
if(!st[j]&&(t==-1||dist[j]<dist[t]))
t=j;
res+=dist[t];
st[t]=true;
for(int j=1;j<=n;j++)
dist[j]=min(dist[j],g[j][t]);
}
return res;
}
Kruskal算法
Kruskal算法是基于并查集的算法，把所有边按照权值排序，然后按照边权从低到高的顺序，对每一条边所连接的两个节点的联通块合并
证明方法同prim类似
const int N = 110,M=210;
struct edge{
int a,b,w;
bool operator<(const edge&e)
{
return w<e.w;
}
} e[M];
int p[N],n,k;
int find(int x) // 并查集
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
int main()
{
cin>>n>>k;
for(int i=1;i<=n;i++) p[i]=i;
for(int i=0;i<k;i++)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
e[i]={a,b,c};
}
sort(e,e+k);
int res=0;
for(int i=0;i<k;i++)
{
int a=find(e[i].a),b=find(e[i].b);
if(a!=b){
p[a]=b;
res+=e[i].w;
}
}
cout<<res<<endl;
}
- 次最小生成树满足的性质
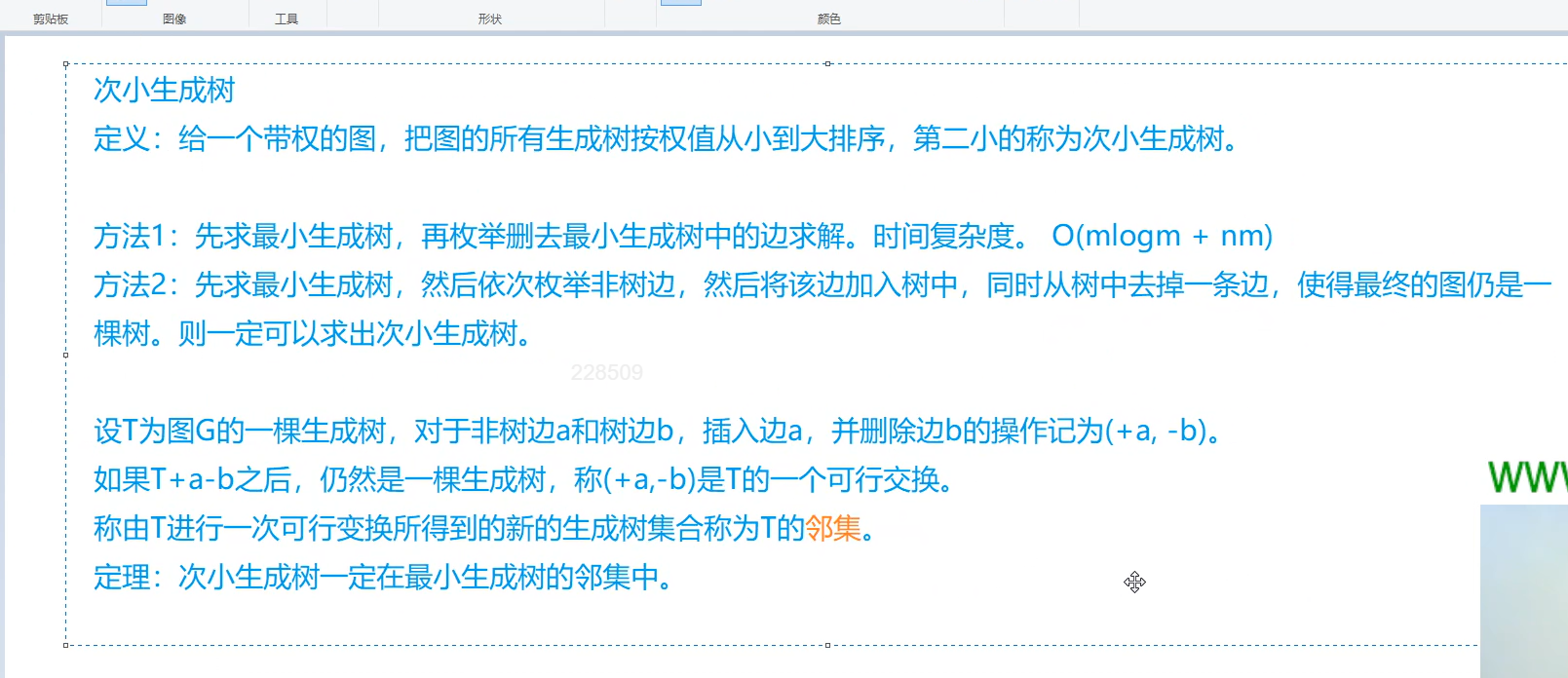
差分约束
对一组不等式组
\(\begin{cases}
x_1\le x_2+c_2\\
x_2\le x_3+c_3\\
\dots \\x_i\le x_j+c_j \\
\end{cases}\)
可以把i和j当作图中的一个顶点，j向i有一条长度为\(c_i\)的边，当我们求图上某一点到点i的最短距离时，一定满足不等式\(dist_i\le dist_j+c_j\),可以对应到上述不等式中去，当不等号方向变过来，则可以求最长路满足不等式\(dist_i\ge dist_j+c_j\)
-
求不等式组的可行解
源点满足条件，从源点出发，一定可以走到所有的边-
1.先将所有的不等式\(x_i\le x_j+ c_j\)，转换成一条从\(x_j走到x_i长度为c_j\)的边
-
2.找到一个超级原点，可以从该点走到所有的边
-
3.从原点求一遍单源最短路，对于小于号的不等式组
如果存在负环，原不等式组一定无解
如果没有负环，那么dist[i]为原方程组的一组可行解证明：如果存在一条负环,则取换上一点\(x_i\),满足条件\(x_i\le x_j+c_j\le x_k+c_j+c_k\le\dots\le x_i+c_j+c_k+c_{\dots}\),右边所有c的和为负数(这些点都是负环上的点)，那么不等式组一定无解
-
-
求最大值或最小值
如果要求上述不等式每一个\(x_i\)的最小或者最大值，那么在方程组中必定有一个或者多个不等式满足\(x_j\le c\),否者求出来的都是x之间的相对关系，没有最小值和最大值
对于\(x_j\le c\),我们可以建立一个虚拟源点\(x_0\)，有该点向\(x_j\)连一条长度为c的边
以求最大值为例，对于图建好之后的任意一点，在源点出发可以到达所有点的前提下，设到点\(x_i\)的最短路径为\(x_0,x_1,x_3,x_{i-1},x_i\),有\(x_i\le x_{i-1}+c_{i-1}\le x_3+c_3+c_{i-1}\le x_1+c_1+c_3+c_{i-1}\le x_0+c_0+c_1+c_3+c_{i-1}\),\(x_0=0\),所以可以得到\(x_i\le d_i\)，\(di\)为从源点到\(x_i\)的一条路径上的总长度，而我们要求最大值，就是找到\(d_i\)的下界，使得所有这样的不等式都成立，即源点到\(x_i\)的最短距离
对应的，当我们要求所有x的最小值的时候，则可以把小于号变成大于号，对称地去求源点出发到所有点的最长距离，就可以找到么一个x对应的最小值acwing1169
- 所有小朋友都要分到糖果，于是有\(x_i\ge1,x_i表示第i个小朋友分到的糖果数\),可以从虚拟源点\(x_0\)向\(x_i\)连边,显然从源点可以遍历到所有的边
要使得分出去的糖果最小，可以让每一个小朋友分到的糖最少，所以这题我们转换成求最长路 - 对于5种请求，转换成大于等于的关系如下：
\(X=1,A\ge B,B\ge A\\X=2,B\ge A+1\\X=3,A\ge B\\X=4,A\ge B+1\\X=5,B\ge A\) - 建好图以后，用spfa求一遍从源点出发到达所有点的最长距离，如果存在正环，则方程组无解，否则，将所有点到源点的最长距离加起来即为最少的糖果数量
- 所有小朋友都要分到糖果，于是有\(x_i\ge1,x_i表示第i个小朋友分到的糖果数\),可以从虚拟源点\(x_0\)向\(x_i\)连边,显然从源点可以遍历到所有的边
-
代码 在用spfa求正环(负环)的时候，用栈存点比队列要来的快
（玄学）#include <iostream> #include <cstring> #include <algorithm> const int N = 1e5+10,M=N*3; using namespace std; int h[N],e[M],ne[M],w[M],idx; bool st[N]; int cnt[N],q[N]; long long dist[N]; int n,k; void add(int a, int b, int c) { e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ; } bool spfa(){ int hh=0,tt=1; memset(dist,-0x3f,sizeof dist); dist[0]=0; q[0]=0; while(hh!=tt){ int t=q[--tt]; st[t]=false; for(int i=h[t];i!=-1;i=ne[i]){ int j=e[i]; if(dist[j]<dist[t]+w[i]){ dist[j]=dist[t]+w[i]; cnt[j]=cnt[t]+1; if(cnt[j]>=n+1) return false; if(!st[j]){ st[j]=true; q[tt++]=j; } } } } return true; } int main() { cin>>n>>k; memset(h, -1, sizeof h); for(int i=1;i<=n;i++){ add(0,i,1); } while(k--){ int x,a,b; cin>>x>>a>>b; if(x==1) add(a,b,0),add(b,a,0); else if(x==2) add(a,b,1); else if(x==3) add(b,a,0); else if(x==4) add(b,a,1); else add(a,b,0); } if(!spfa()) cout<<"-1"<<endl; else { long long res=0; for(int i=1;i<=n;i++){ res+=dist[i]; } cout<<res<<endl; } return 0; }
Lca
朴素做法
每次查询时间复杂度\(O(n)\),不再赘述
int lca(int a,int b){//预处理出深度
if(depth[a]<depth[b]) swap(a,b);
while(depth[a]>depth[b]) a=fa[a];
if(a==b) return a;
while(a!=b) a=fa[a],b=fa[b];
return a;
}
倍增法
利用二进制拆分的思想，对每个点i，预处理出来从i向上走\(2^j\)步的节点,有递推式
\[fa[i][j]=fa[fa[i][j-1]]\\
\text{初始条件}\ fa[i][0]=i\text{的父节点}
\]
这样可以用\(O(nlog_2(n))\)的时间预处理每个点的深度\(depth[i]\)和向上走\(2^j\)步的节点\(fa[i][j]\)
每次查询两点\(a\)和\(b\)的公共祖先时，先让\(a\)和\(b\)深度较大的一个点向上跳，从高到底枚举向上跳的步数的长度k,只要满足\(depth[fa[a][k]]>=depth[b]\),就让a向上跳，即\(a=fa[a][k]\)
此时\(a\)和\(b\)的深度相同，当\(a=b\)时，lca函数直接返回\(a\)，否则，在再分别枚举k，让\(a\)和\(b\)同时向上跳，直到\(fa[a][0]==fa[b][0]\),这时返回\(fa[a][0]\)
代码 预处理复杂度\(O(nlog(n))\),每次查询复杂度\(O(log(n))\)
const int N = 4e4+10,M=2*N;
int h[N], e[M], ne[M], idx;
int depth[N],fa[N][17];\\17是log2(N)
void bfs(int root){\\预处理
memset(depth,0x3f,sizeof depth);
depth[0]=0,depth[root]=1;
queue<int>q;
q.push(root);
while(q.size()){
auto t=q.front();
q.pop();
for(int i=h[t];i!=-1;i=ne[i]){
int j=e[i];
if(depth[j]>depth[t]+1){
depth[j]=depth[t]+1;
q.push(j);
fa[j][0]=t;
for(int k=1;k<=15;k++)
fa[j][k]=fa[fa[j][k-1]][k-1];
}
}
}
}
int lca(int a,int b){
if(depth[a]<depth[b]) swap(a,b);
for(int k=15;k>=0;k--){
if(depth[fa[a][k]]>=depth[b])
a=fa[a][k];
}
if(a==b) return b;
for(int k=15;k>=0;k--){
if(fa[a][k]!=fa[b][k])
{
a=fa[a][k];
b=fa[b][k];
}
}
return fa[a][0];
}
tarjan求lca
有空再写
acwing 1171代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
#define x first
#define y second
using namespace std;
const int N = 1e4+10,M=2*N;
int h[N], e[M], ne[M], idx,w[M];
int p[N],d[N];
typedef pair<int, int> PII;
vector<PII>query[N];
int st[N],res[M];
int find(int x) // 并查集
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
void add(int a, int b, int c) // 添加一条边a->b，边权为c
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs(int u,int fa){
for(int i=h[u];i!=-1;i=ne[i]){
int j=e[i];
if(j==fa) continue;
d[j]=d[u]+w[i];
dfs(j,u);
}
}
void tarjan(int u){
st[u]=1;
for(int i=h[u];i!=-1;i=ne[i]){
int j=e[i];
if(!st[j])
{
tarjan(j);
p[j]=u;
}
}
for(auto t:query[u]){
int y=t.x,id=t.y;
if(st[y]==2)
{
int ans=find(y);
res[id]=d[u]+d[y]-2*d[ans];
}
}
st[u]=2;
}
int main()
{
int n,m;
cin>>n>>m;
memset(h, -1, sizeof h);
for(int i=1;i<n;i++){
int a,b,c;
cin>>a>>b>>c;
add(a,b,c),add(b,a,c);
}
for(int i=1;i<=m;i++){
int x,y;
cin>>x>>y;
if(x!=y){
query[x].push_back({y,i});
query[y].push_back({x,i});
}
}
dfs(1,-1);
for(int i=1;i<=n;i++) p[i]=i;
tarjan(1);
for(int i=1;i<=m;i++) cout<<res[i]<<endl;
return 0;
}
树上差分
树上差分分为对点和对边进行差分，其核心思想和一维数组的差分类似
-
对点的差分
对于一棵树上两点\(x\)和\(y\),要使得从\(x\)到\(y\)上的路径上的点都加上一个常数c,只需要对每个点建立一个差分数组d,每次操作，只需要\[d[x]+=c,d[y]+=c,d[lac(x,y)]-=c,d[fa[lca(x)][0]]-=c \] -
对边的差分
对于一棵树上两点\(x\)和\(y\),要使得从\(x\)到\(y\)上的路径上的边都加上一个常数c,将边缩成点，用每条边深度较大的那个点来表示这条边，对每个点，建立差分数组，每次操作，令\[d[x]+=c,d[y]+=c,d[lca(x,y)]-=2c \]
有向图的强连通分量（SCC)
tarjan缩点
在对每个强连通分量缩点之后，按照强连通分量的编号递减的顺序就是拓扑序
const int N = 1e5+10,M=2*N;
int h[N],hs[N],e[M], ne[M], idx,w[M];
int dfn[N], low[N], timestamp; // 时间戳
int stk[N], top;
bool in_stk[N];
int id[N], scc_cnt,scc_size[N]; // 每个点所属分量编号
void tarjan(int u)
{
dfn[u] = low[u] = ++ timestamp;
stk[ ++ top] = u, in_stk[u] = true;
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if (!dfn[j])
{
tarjan(j);
low[u] = min(low[u], low[j]);
}
else if (in_stk[j]) low[u] = min(low[u], dfn[j]);
}
if (dfn[u] == low[u])
{
++ scc_cnt;
int y;
do {
y = stk[top -- ];
in_stk[y] = false;
id[y] = scc_cnt;
scc_size[scc_cnt] ++ ;
} while (y != u);
}
}
无向图的双联通分量（DCC)
几个概念:
- 桥\割边：将某一条边删除会使得一个连通块变成两个连通块，这样的边成为桥
- 边联通分量：不包含桥的联通图称为边联通分量
- 割点：将一个点和与该点相关的所有边上删去，会使得一个联通图变成多个连通块，称作割点
- 点联通分量：对于自生来说，不含有割点的连通图（可能含有一张更大的图的割点）
割边、边联通分量
在无向图中，不存在横插边
判断一个边（\(u->j\)）是否为桥的条件是
\[dfn[u]<low[j],\text{则是桥}
\]
代码
int h[N], e[M], ne[M], idx;
int dfn[N], low[N], timestamp; // 时间戳
int stk[N], top;
int id[N], dcc_cnt,d[N]; // 每个点所属分量编号
bool is_bridge[M];
void add(int a, int b) // 添加一条边a->b
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void tarjan(int u,int from){
dfn[u]=low[u]=++timestamp;
stk[++top]=u;
for(int i=h[u];~i;i=ne[i]){
int j=e[i];
if(!dfn[j]){
tarjan(j,i);
low[u]=min(low[u],low[j]);
if(dfn[u]<low[j])
is_bridge[i]=is_bridge[i^1]=true;//对一条边来说，如果i为偶数，那么i的反向边i+1，如果为奇数，反向边i+1,所以为i^1
}
else if(i!=(from^1))
low[u]=min(low[u],dfn[j]);
}
if(low[u]==dfn[u]){
int y;
dcc_cnt++;
do{
y=stk[top--];
id[y]=dcc_cnt;
}while(y!=u);
}
}
//这段代码不仅求出了边双联通分量，还求出了哪些边是割边
割点、点联通分量
求割点
判断一个点是否为割点的条件是
如果点不是根节点，那么只要满足\(low[j]\ge dfn[u]\),那么就是割点，如果是根节点，那么如果以该根节点存在两颗以上的子树，那也是割点
题目 洛谷p3388
给出一个 n 个点，m 条边的无向图，求图的割点。
代码
#include <iostream>
#include <cstring>
#include<vector>
#include <algorithm>
using namespace std;
const int N=2e4+10;
vector<int> e[N];
int dfn[N],low[N],timestamp;
bool cut[N];
void tarjan(int u,int root){
dfn[u]=low[u]=++timestamp;
int child=0;
for(auto v:e[u]){
if(!dfn[v])
{
tarjan(v,root),low[u]=min(low[u],low[v]);
if(low[v]>=dfn[u]&&u!=root) cut[u]=true;
if(u==root) child++;
}
else low[u]=min(low[u],dfn[v]);
}
if(u==root&&child>=2) cut[u]=true;
}
int main()
{
int n,m;
cin>>n>>m;
while(m--){
int a,b;
cin>>a>>b;
e[a].push_back(b);
e[b].push_back(a);
}
for(int i=1;i<=n;i++)
if(!dfn[i]) tarjan(i,i);
int sum=0;
for(int i=1;i<=n;i++) if(cut[i]) sum++;
cout<<sum<<endl;
for(int i=1;i<=n;i++) if(cut[i]) cout<<i<<" ";
}
二分图
一个图是二分图$\Leftrightarrow \(不存在奇数环\)\Leftrightarrow$染色法不存在矛盾
匈牙利算法（二分图的最大匹配）
最大匹配\(\Leftrightarrow\)不存在增广路径
增广路径：从一个非匹配点走，按照非匹配边\(\rightarrow\)匹配边\(\rightarrow\)非匹配边的顺序，走到一条非匹配点
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 5e2+10,M=1e5+10;
int h[N], e[M], ne[M], idx;
bool st[N];
int match[N];
void add(int a, int b) // 添加一条边a->b
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
int find(int u){
for(int i=h[u];~i;i=ne[i]){
int j=e[i];
if(!st[j]){
st[j]=true;
if(!match[j]||find(match[j])) {
match[j]=u;
return true;
}
}
}
return false;
}
int main()
{
int n1,n2,m;
cin>>n1>>n2>>m;
memset(h, -1, sizeof h);
for(int i=1;i<=m;i++){
int a,b;
cin>>a>>b;
add(a,b);
}
int res=0;
for(int i=1;i<=n1;i++) {
memset(st, 0, sizeof st);
if(find(i)) res++;
}
cout<<res<<endl;
}
最小点覆盖
在一张二分图中，给定的若干条边中，选择边两端的一些点，使得每条边上至少有一个点被覆盖，称为二分图的最小点覆盖问题
最小点覆盖数=二分图的最大匹配数
证明待
最大独立集
在一个图中，含有的最多的任意两点之间没有边的点的集合，称为最大独立集
最大团 含有的最多的任意两点之间都有边的点的集合，和最大独立集为互补的关系
最大独立集\(\ =\)最大团\(\ =\)总点数\(-\)最大匹配数
最小路径覆盖
对一个有向无环图，使用最少的不相交路径(既没有重复的点也没有重复的边)，使得所有的点都被覆盖,称作最小路径覆盖
结论：最小路径点覆盖=总点数-最大匹配数
利用拆点的方法证明
最小重复路径点覆盖：对原图\(G\)求一遍传递闭包，得到\(G'\)，然后对\(G'\)求一遍最小路径覆盖，就可以得到G的最小重复路径点覆盖。
树上倍增
树上倍增维护区间最 大/小 和 cf 1843 f2
使用了动态建立st表的方式
#include <iostream>
#include <cstring>
#include<string>
#include <map>
#include<cmath>
#include<vector>
#include<queue>
#include <algorithm>
#include<unordered_map>
#include<set>
#include<map>
#include<functional>
#include<fstream>
#include<sstream>
#define x first
#define y second
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
const int N=2e5+10;
struct node{
int lmax,rmax;
int lmin,rmin;
int mi,mx;
int sum;
node(){
lmax=rmax=lmin=rmin=mi=mx=sum=0;
}
node operator+(node&v){
node r;
r.mx=max({mx,v.mx,rmax+v.lmax});
r.mi=min({mi,v.mi,rmin+v.lmin});
r.lmax=max(lmax,sum+v.lmax);
r.lmin=min(lmin,sum+v.lmin);
r.rmax=max(v.rmax,v.sum+rmax);
r.rmin=min(v.rmin,v.sum+rmin);
r.sum=sum+v.sum;
return r;
}
void rev(){//一个子段反转
swap(lmax,rmax);
swap(rmin,lmin);
}
static node get_root (int x){
node t;
t.lmax=t.rmax=t.mx=max(0,x);
t.rmin=t.lmin=t.mi=min(0,x);
t.sum=x;
return t;
}
};
node dp[N][19];
int fa[N][19],depth[N];
void ins(int x,int v,int u)//动态构建st表
{
if(x!=1) depth[x]=depth[v]+1;
fa[x][0]=v;
dp[x][0]=node::get_root(u);
for(int i=1;i<19;i++)
{
fa[x][i]=fa[fa[x][i-1]][i-1];
dp[x][i]=dp[x][i-1]+dp[fa[x][i-1]][i-1];
}
}
node lca(int a,int b){
node res1,res2;
if(depth[a]<depth[b])
swap(a,b);
for(int i=18;i>=0;i--)
if(depth[a]-(1<<i)>=depth[b])
res1=res1+dp[a][i],a=fa[a][i];
if(a==b) return res1+dp[a][0];
for(int i=18;i>=0;i--)
{
if(fa[a][i]!=fa[b][i])
{
res1=res1+dp[a][i],res2=res2+dp[b][i];
a=fa[a][i],b=fa[b][i];
}
}
res1=res1+dp[a][0];
res2=res2+dp[b][0];
res2.rev();
a=fa[a][0];
return res1+dp[a][0]+res2;
}
void solve(){
int n,cnt=1;
cin>>n;
ins(1,1,1);
while(n--){
char op;
cin>>op;
if(op=='+'){
int p,x;
cin>>p>>x;
ins(++cnt,p,x);
}
else {
int u,v,k;
cin>>u>>v>>k;
node t=lca(u,v);
if(k<t.mi||k>t.mx) cout<<"NO"<<endl;
else cout<<"YES"<<endl;
}
}
}
int main()
{
int t;
cin>>t;
while(t--) solve();
}
动态规划
单调队列优化dp
单调队列优化多重背包问题
洛谷P1833
#include <iostream>
using namespace std;
const int N=1e5+10;
int s[N],w[N],v[N],f[2][1010],q[N];
int main()
{
int sh,sm,eh,em,n;
scanf("%d:%d %d:%d%d",&sh,&sm,&eh,&em,&n);
int m=eh*60+em-sh*60-sm;
for(int i=1;i<=n;i++) cin>>v[i]>>w[i]>>s[i];
for(int i=1;i<=n;i++)
{
if(s[i]==0){
for(int j=0;j<=m;j++)
if(j<v[i]) f[i&1][j]=f[i-1&1][j];
else f[i&1][j]=max(f[i&1][j-v[i]]+w[i],f[i-1&1][j]);
}
else {
for(int r=0;r<v[i];r++){
int hh=0,tt=-1;
for(int j=r;j<=m;j+=v[i]){
while(hh<=tt&&j-q[hh]>s[i]*v[i]) hh++;
while(hh<=tt&&f[i-1&1][q[tt]]+(j-q[tt])/v[i]*w[i]<=f[i-1&1][j]) tt--;
q[++tt]=j;
f[i&1][j]=f[i-1&1][q[hh]]+(j-q[hh])/v[i]*w[i];
}
}
}
}
cout<<f[n&1][m]<<endl;
}
数位dp
记忆化搜索数位dp
acwing 4639
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 20;
LL f[N][N][N*1000];
int a[N];
LL dfs(int pos,bool lim,bool lead0,int val,int mid){
if(val<0) return 0;
if(!pos) return !val&&!lead0;
auto &t=f[pos][mid][val];
if(~t&&!lim&&!lead0) return t;
int up=lim?a[pos]:9;
LL res=0;
for(int i=0;i<=up;i++)
res+=dfs(pos-1,lim&&i==up,lead0&&i==0,val+(pos-mid)*i,mid);
if(!lim&&!lead0) t=res;
return res;
}
LL dp(LL n){
int len=0;
while(n) a[++len]=n%10,n/=10;
LL res=0;
for(int i=1;i<=len;i++) res+=dfs(len,true,true,0,i);
return res;
}
int main()
{
int t;
cin>>t;
memset(f,-1,sizeof f);
while(t--){
LL l,r;
cin>>l>>r;
LL res=0;
if(l!=0) res=dp(r)-dp(l-1);
else res=dp(r)+1;
cout<<res<<endl;
}
}
树形dp
树上背包问题
当定义\(dp\)数组中的第二维和子树的大小有关时，就可以将树上背包问题优化到\(O(n^2)\)
2020 icpc 南京H题
代码
#include <iostream>
#include <cstring>
#include<string>
#define x first
#define y second
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
typedef pair<LL,int> PLI;
const int N=2e3+10;
const long long INF=1e18;
vector<int>son[N];
LL f[N][N][2];
int h[N],sz[N];
void dfs(int u){
static LL tem[N][2];
f[u][0][0]=h[u];
f[u][1][0]=f[u][0][1]=INF;
f[u][1][1]=0;
sz[u]=1;
for(auto v:son[u]){
dfs(v);
for(int i=0;i<=sz[u]+sz[v];i++) tem[i][0]=tem[i][1]=INF;
for(int i=0;i<=sz[u];i++)
for(int j=0;j<=sz[v];j++)
{
tem[i+j][0]=min(tem[i+j][0],f[u][i][0]+f[v][j][1]);
tem[i+j][0]=min(tem[i+j][0],f[u][i][0]+f[v][j][0]+h[v]);
tem[i+j][1]=min(tem[i+j][1],f[u][i][1]+min(f[v][j][0],f[v][j][1]));
}
for(int i=0;i<=sz[u]+sz[v];i++)
f[u][i][0]=tem[i][0],f[u][i][1]=tem[i][1];
sz[u]+=sz[v];
}
}
void solve(){
int n;
cin>>n;
for(int i=1;i<=n;i++) son[i].clear();
for(int i=2;i<=n;i++)
{
int p;
cin>>p;
son[p].push_back(i);
}
for(int i=1;i<=n;i++) cin>>h[i];
dfs(1);
for(int i=0;i<=n;i++)
cout<<min(f[1][i][0],f[1][i][1])<<" ";
cout<<endl;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int T;
cin>>T;
while(T--) solve();
}
acwing 10 有依赖的背包问题
有 N 个物品和一个容量是 V的背包，物品之间具有依赖关系，且依赖关系组成一棵树的形状。如果选择一个物品，则必须选择它的父节点，求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。输出最大价值。
-
\(O(nm^2)\)做法
\(f[i][j]\)表示给以i为根的子树,且必须包含节点i，分配\(j\) 容量的最大价值，状态转移为：\[f[i][j]=max(f[i][j],f[i][k]+f[son][k]) \\其中，son为i的子节点，j>=w[i] \]代码
#include<iostream> #include<cstring> using namespace std; const int N=110; int h[N],ne[N],e[N],w[N],v[N],idx=0,f[N][N]; int n,m; void add(int a,int b) { e[idx]=b; ne[idx]=h[a]; h[a]=idx++; } void dfs(int u) { for(int j=v[u];j<=m;j++) f[u][j]=w[u]; //初始化，只要能选择第u个节点，就起码有选择第u个节点价值 for(int i=h[u];i!=-1;i=ne[i]) { int son=e[i]; dfs(son); //先计算u的一个子树 for(int j=m;j>=v[u];j--) //因为至少要为u分配v[u]个大小的体积 for(int k=0;k<=j-v[u];k++) //对每个叶节点分配的大小 f[u][j]=max(f[u][j],f[u][j-k]+f[son][k]); } } int main() { cin>>n>>m; memset(h,-1,sizeof h); int root=0; for(int i=1;i<=n;i++) { int a; scanf("%d%d%d",&v[i],&w[i],&a); if(a==-1) root=i; else add(a,i); } dfs(root); cout<<f[root][m]; }- dfs序优化,\(O(nm)\)
利用dfs序，将树上背包问题转换成线性的背包问题
状态定义：\(f[i][j]\)表示给按照dfs序的顺序，\(i到n\)的所有节点，分配大小\(j\)的体积，可得到的最大价值记\(dfs的第i个\)节点对应的原始的编号为\(id[i]\),记作\(u\), \(r[u]\)表示节点\(u\)所在的子树中最后一个节点的dfs序
状态转移：
\[f[i][j]=max(f[r[u]+1][j],f[i+1][j-v[i]]+w[i]) \]前一个表示不选当前节点，那么该节点所对应的子树都不能选，所以要由状态\(f[r[u]+1][j]\)转移过来
后一个表示选择当前的节点。很显然，时间复杂度是\(O(n^2)\)的
代码
#include<iostream> #include<cstring> using namespace std; const int N=110,INF=1<<30; int h[N],ne[N],e[N],v[N],w[N],idx=0,f[N][N]; int l[N],r[N],tot,id[N];//求dfs序 int n,m; void add(int a,int b) { e[idx]=b; ne[idx]=h[a]; h[a]=idx++; } void dfs(int u)//求dfs序 { l[u]=++tot;//u所对应的dfs序 id[tot]=u; for(int i=h[u];~i;i=ne[i]){ int j=e[i]; dfs(j); } r[u]=tot;//该子树的最后一个节点所对应的dfs序 } int main() { cin>>n>>m; memset(h,-1,sizeof h); int root=0; for(int i=1;i<=n;i++) { int a; scanf("%d%d%d",&v[i],&w[i],&a); if(a==-1) root=i; else add(a,i); } dfs(root); //for(int i=1;i<N;i++) f[n+1][i]=-INF; for(int i=n;i;i--){ int u=id[i]; for(int j=0;j<=m;j++){ f[i][j]=f[r[u]+1][j];//不选该子树和对应的所有节点 if(j>=v[u]) f[i][j]=max(f[i][j],f[i+1][j-v[u]]+w[u]); } } cout<<f[1][m]<<endl; }
线性DP推公式
洛谷 P3558 BAJ-Bytecomputer
题目描述给定一个长度为 nn 的只包含 -1,0,1−1,0,1 的数列 aa，每次操作可以使 \(a_i=a_i+a_{i-1}\),求最少操作次数使得序列单调不降。如果不可能通过该操作使得序列单调不降，请输出 BRAK。
数据范围：1≤n≤106
这题主要是推公式，\(f[i][j]\)表示把序列中的第1~i个数，变成一个单调不降序列的最小操作数，j表示状态，j=0,1,2表示把第i个数改成-1，0，1，分九种情况讨论
- nums[i]=-1
\(f[i][0]=f[i-1][0]\)
$f[i][1]=min(f[i-1][0],f[i-1][1])+1 $ $ if\ \ nums[i-1]=1$
\(=INF\;if\;nums[i-1]\ne 1\)
\(f[i][2]=min(f[i-1][0],f[i-1][1],f[i-1][2])+2\ \ if\ nums[i-1]=1\)
\(f[i-1][2]+2\ \ if\ nums[i-1]\ne1\)
-
nums[i]=0
\(f[i][0]=f[i-1][0]+1\)
\(f[i][1]=min(f[i-1][0],f[i-1][1])\)
\(f[i][2]=min(f[i-1][0],f[i-1][1],f[i-1][2])+1\ \ if\ nums[i-1]=1\)
\(f[i-1][2]+1\ \ if\ nums[i-1]\ne1\) -
nums[i]=1
\(f[i][0]=f[i-1][0]+2\)
\(f[i][1]=min(f[i-1][0],f[i-1][1])+1\ if\ nums[i-1]=-1\)
\(=f[i-1][0]+1 \ if\ nums[i-1]\ne-1\)
\(f[i][2]=min(f[i-1][0],f[i-1][1],f[i-1][2])\)终于推完了C++代码
#include<iostream> #include<cstring> #include<vector> #include<cmath> #include<algorithm> using namespace std; const int N=1e6+10,INF=0x3f3f3f3f; int f[N][3]; int a[N]; int main() { int n; cin>>n; for(int i=1;i<=n;i++) scanf("%d",&a[i]); f[1][0]=f[1][1]=f[1][2]=INF; f[1][a[1]+1]=0; for(int i=2;i<=n;i++) { f[i][0]=f[i-1][0]+a[i]+1; if(a[i]==-1) { if(a[i-1]==1){ f[i][1]=min(f[i-1][1],f[i-1][0])+1; f[i][2]=min(f[i-1][0],min(f[i-1][1],f[i-1][2]))+2; } else { f[i][1]=INF; f[i][2]=f[i-1][2]+2; } } else if(a[i]==0) { f[i][1]=min(f[i-1][0],f[i-1][1]); if(a[i-1]==1) f[i][2]=min(f[i-1][0],min(f[i-1][1],f[i-1][2]))+1; else f[i][2]=f[i-1][2]+1; } else{ f[i][2]=min(f[i-1][0],min(f[i-1][2],f[i-1][1])); if(a[i-1]==-1) { f[i][1]=min(f[i-1][1],f[i-1][0])+1; } else f[i][1]=f[i-1][0]+1; } } int res=min(f[n][0],min(f[n][1],f[n][2])); if(res>=INF) printf("BRAK\n"); else cout<<res<<endl; }
用贪心+dp
acwing 277 饼干
圣诞老人共有 M 个饼干，准备全部分给 N 个孩子。
每个孩子有一个贪婪度，第 i 个孩子的贪婪度为 g[i]。
如果有 a[i] 个孩子拿到的饼干数比第 i 个孩子多，那么第 i 个孩子会产生 g[i]×a[i] 的怨气。
给定 N、M 和序列 g，圣诞老人请你帮他安排一种分配方式，使得每个孩子至少分到一块饼干，并且所有孩子的怨气总和最小。
输入格式
第一行包含两个整数 N,M。
第二行包含 N 个整数表示 g1∼gN。
输出格式
第一行一个整数表示最小怨气总和。
第二行 N 个空格隔开的整数表示每个孩子分到的饼干数，若有多种方案，输出任意一种均可。
数据范围
1≤N≤30,
N≤M≤5000,
1≤gi≤107
输入样例：
3 20
1 2 3
输出样例：
2
2 9 9
- 排序不等式：
\(0\le a_1\le a_2\le \cdots\le a_n\)，\(0\le b_1\le b_2\le \cdots\le b_n\)
有\(a_1b_n+a_2b_{n-1}+\cdots+a_nb_1\le a_1b_{i-1}+a_2b_{i_2}+\cdots+a_nb_{i_n}\le a_1b_1+a_2b_{2}+\cdots+a_nb_n\)
其中i1,i2……in 是b的任意一种排列，可以通过调整法证明,概括一下就是：
\(逆序\le 乱序\le 顺序\)
因此在给小孩分配饼干时，应该要让\(g[i]\)越大的小孩，分配到的饼干越多，\(a_{i}\)越小，所以要将g[i]先排个序，大的在前面
-
状态表示和转换
定义\(f[i][j]\)为对排序后的前i个小孩，分配j个饼干的贪婪值总和
按照当前状态下，有几个小孩分到了一块饼干进行状态划分：-
有k个小孩分配到一个一块饼干(\(1\le k\le min(i,j)\)),有\(f[i][j]=min(f[i][j],f[i-k][j-k]+(i-k)*(s[i]-s[i-k]))\)
s为排好序后的\(g数组\)的前缀和 -
没有小孩分配到一块饼干
由于前i个小孩的大小关系已经确定，我们可以做一次映射，让每个孩子的饼干都减去1，这样相对关系仍然不变，因此有
\(f[i][j]=f[i][j-i],(j\ge i)\)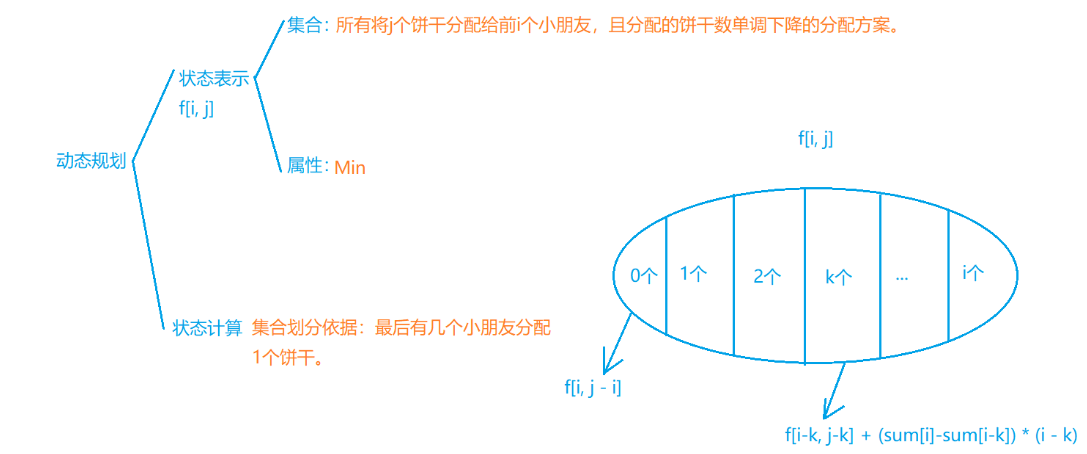
-
-
最后求每个小朋友分配到的饼干数，从\(f[n][m]\)向前推，当\(f[i][j]==f[i][j-i]\)时，要加上1的偏移量，可以通过一个变量h来存储
C++代码
#include <iostream> #include <cstring> #include <algorithm> #include <queue> #include<unordered_map> #define x first #define y second using namespace std; typedef long long LL; const int N = 35,M=5e3+10; typedef pair<int,int> PII; PII g[N]; int f[N][M]; int ans[N]; int s[N]; int main() { int n,m; cin>>n>>m; for(int i=1;i<=n;i++) { scanf("%d",&g[i].x); g[i].y=i; } sort(g+1,g+1+n); reverse(g+1,g+1+n); memset(f,0x3f,sizeof f); f[0][0]=0; for(int i=1;i<=n;i++) s[i]=s[i-1]+g[i].x; for(int i=1;i<=n;i++) { for(int j=i;j<=m;j++)//每个孩子至少一个饼干 { f[i][j]=f[i][j-i]; for(int k=1;k<=i&&k<=j;k++) f[i][j]=min(f[i][j],f[i-k][j-k]+(s[i]-s[i-k])*(i-k)); } } cout<<f[n][m]<<endl; int i=n,j=m,h=0; while(i&&j) { if(j>=i&&f[i][j]==f[i][j-i]) h++,j-=i; else { for(int k=1;k<=i&&k<=j;k++) { if(f[i][j]==f[i-k][j-k]+(s[i]-s[i-k])*(i-k)) { for(int u=i;u>i-k;u--) { ans[g[u].y]=h+1; } i-=k,j-=k; break; } } } } for(int i=1;i<=n;i++) cout<<ans[i]<<" "; }
斜率优化的动态规划问题
acwing 301 任务安排2
题目描述
有 N 个任务排成一个序列在一台机器上等待执行，它们的顺序不得改变。机器会把这 N 个任务分成若干批，每一批包含连续的若干个任务。从时刻 0 开始，任务被分批加工，执行第 i 个任务所需的时间是 Ti。另外，在每批任务开始前，机器需要 S 的启动时间，故执行一批任务所需的时间是启动时间 S 加上每个任务所需时间之和。一个任务执行后，将在机器中稍作等待，直至该批任务全部执行完毕。
也就是说，同一批任务将在同一时刻完成。每个任务的费用是它的完成时刻乘以一个费用系数 Ci。请为机器规划一个分组方案，使得总费用最小。
输入格式
输入格式
第一行包含整数 N。
第二行包含整数 S。
接下来 N 行每行有一对整数，分别为 Ti 和 Ci，表示第 i 个任务单独完成所需的时间 Ti 及其费用系数 Ci。
输出格式
输出一个整数，表示最小总费用。
数据范围
1≤N≤3×105,
1≤Ti,Ci≤512,
0≤S≤512
-
朴素版本状态转移方程
\(f[i]\)表示以第i个机器结尾的总费用,\(sc\)和\(st\)分别为费用系数和执行时间的前缀和
\(f[i]=f[j]+S*(sc[n]-sc[j])+st[i]*(sc[i]-sc[j]); 0\le j<i\) -
朴素版本的时间复杂度为\(O(n^2)\)，现在考虑用凸包算法优化，上述公式i为常量，j为变量
\(f[j]=sc[j]*(S+st[i])+(f[i]-st[i]*sc[i]-S*sc[n])\)
把\(f[j]\)看成\(y\),\(sc[j]\)看成x,该公式可以表示为\(y=k*x+b\)的形式，其中截距b中，f[i]是我们要求的值，k为常数
原问题转化为在\((sc[j],f[j])\) 表示的点的集合中，找到一条截距最小的直线
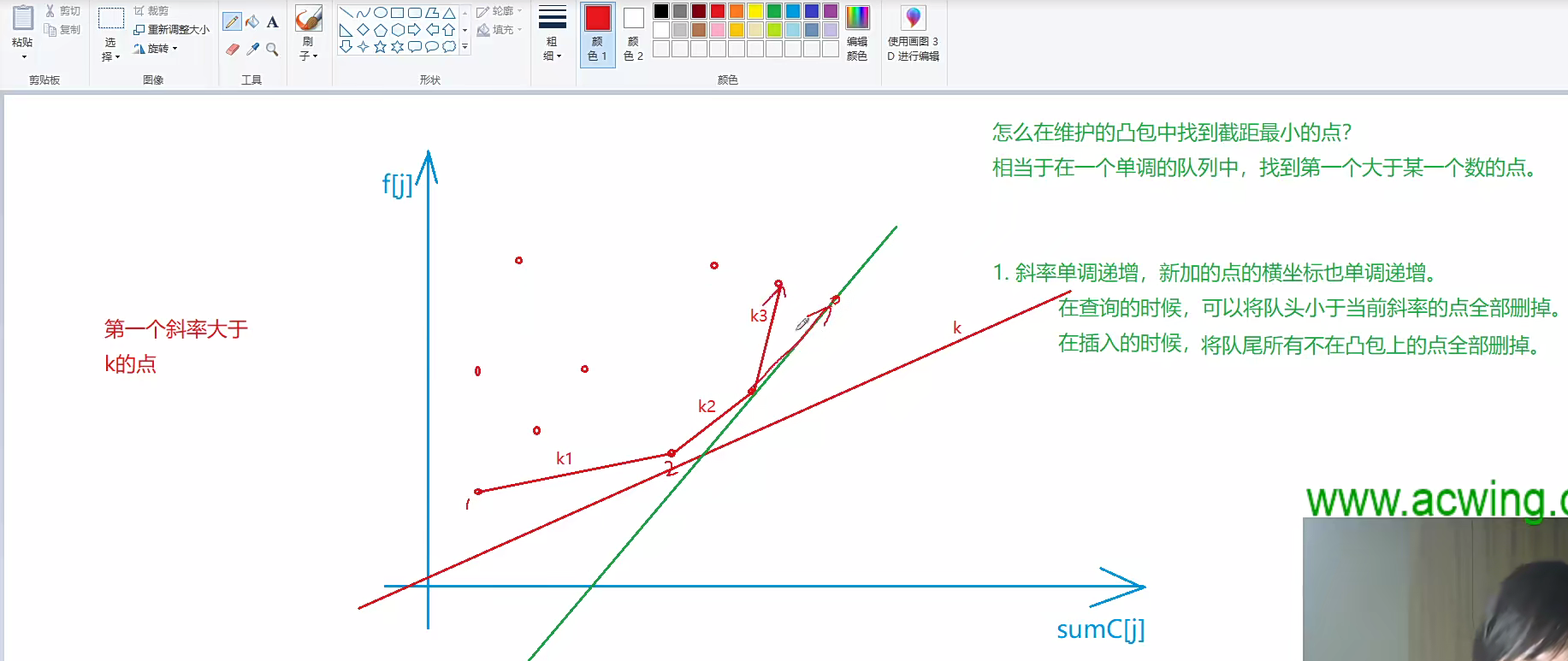
截距最小的点一定在凸包中的下边界，每次都要找到第一个斜率大于当前斜率的点
利用单调队列的思想，随着i的增加，满足两个性质
-
斜率 k（\(S+st[i]\)）递增，且永远为正数
因此我们可以将队头小于当前斜率的点全部删掉
计算队头斜率 \(\frac{f[q[hh+1]]-f[q[hh]]}{sc[q[hh+1]]-sc[q[hh]]}\) -
插入的点在点集的最右侧（
看图就行），从队尾开始，所有斜率大于当前斜率的点都被删掉
计算队尾斜率\(\frac{f[q[tt]]-f[q[tt-1]]}{sc[q[tt]]-sc[q[tt-1]]}\)C++代码
#include<iostream>
#include<cstring>
#include<vector>
#include<cmath>
#include<algorithm>
using namespace std;
const int N=3e5+10;
long long sc[N],st[N],f[N],q[N];
int main()
{
int n,s;
cin>>n>>s;
for(int i=1;i<=n;i++)
{
scanf("%lld%lld",&st[i],&sc[i]);
st[i]+=st[i-1];
sc[i]+=sc[i-1];
}
int hh=0,tt=0;
q[hh]=0;
for(int i=1;i<=n;i++)
{
while(hh<tt&&(f[q[hh+1]]-f[q[hh]])<(s+st[i])*(sc[q[hh+1]]-sc[q[hh]])) hh++;//这里要注意，队头用while，和滑动窗口不一样
int j=q[hh];
f[i]=f[j]+s*(sc[n]-sc[j])+st[i]*(sc[i]-sc[j]);
while(hh<tt&&(f[q[tt]]-f[q[tt-1]])*(sc[i]-sc[q[tt]])>(f[i]-f[q[tt]])*(sc[q[tt]]-sc[q[tt-1]]))
tt--;
q[++tt]=i;
}
cout<<f[n]<<endl;
}
acwing 302 任务安排3
这题和上一题，数据范围有一点变化
数据范围
1≤N≤3×105,
0≤S,Ci≤512,
−512≤Ti≤512
由于Ti变成了正负数，因此上题的第一个性质：斜率 k（\(S+st[i]\)）递增，且永远为正数 不满足
可以利用二分在当前点集中找到第最小的一个点x,满足以下性质：
\(\frac {f[x+1]-f[x]}{sc[x+1]-sx[x]}\le S+st[i]\)
C++代码
最后一个测试点会爆long long ，第一次知道double是用科学计数法存储的，存储范围比long long大的多，最大能到308位数字，1.79e308 ~ +1.79e308，long long是19位
#include<iostream>
#include<cstring>
#include<vector>
#include<cmath>
#include<algorithm>
using namespace std;
const int N=3e5+10;
long long sc[N],st[N],f[N],q[N];
int main()
{
int n,s;
cin>>n>>s;
for(int i=1;i<=n;i++)
{
scanf("%lld%lld",&st[i],&sc[i]);
st[i]+=st[i-1];
sc[i]+=sc[i-1];
}
int hh=0,tt=0;
q[hh]=0;
for(int i=1;i<=n;i++)
{
int l=hh,r=tt;
while(l<r)
{
int mid=l+r>>1;
if((f[q[mid+1]]-f[q[mid]])>(s+st[i])*(sc[q[mid+1]]-sc[q[mid]])) r=mid;
else l=mid+1;
}
int j=q[r];
f[i]=f[j]+s*(sc[n]-sc[j])+st[i]*(sc[i]-sc[j]);
while(hh<tt&&(double)(f[q[tt]]-f[q[tt-1]])*(sc[i]-sc[q[tt]])>=(double)(f[i]-f[q[tt]])*(sc[q[tt]]-sc[q[tt-1]]))
tt--;
q[++tt]=i;
}
printf("%lld",f[n]);
}
acwing 303 运输小猫
分析
首先可以预处理出来一个前缀和\(S_i\), 表示第一座山到第i座山的距离，对第i只猫，要使一个饲养员能接到它，饲养员出发的时间必须满足
\(t_i\ge Ti-Si\),设\(t_i\)为要接到该猫饲养员出发的最早时间，饲养员实际的出发时间表示为\(t_i+\Delta t\),那么猫等待的时间就是\(t_i+\Delta t -(Ti-Si)\)，用\(a_i\)表示\(T_i-S_i\),把\(a_i\)排个序，从左到右饲养员要接到该猫，最早出发的时间依次递增
饲养员接猫的顺序，应该是从该序列里自左向右，一段一段接的。
- 状态表示
\(f[j][i]\)表示第前j个饲养员，接到1~i 的所有猫的总等待时间（P小于N，尽量让矩阵最后一维的空间最大，这样访问的空间越连续）
设第前j-1 个饲养员接到的猫范围为k(\(k<i\)),那么第 j 个饲养员要接的猫就是k+1到 j, 第 j -1个饲养员出发的时间可以取的范围是\(a[k]\le t_{j-1}<a[k+1]\),显然要是总等待时间最少，\(t_{j-1}\)应该取\(a[k]\)，多了没有意义。第j个饲养员出发的时间 满足\(a[i]\le t_j<a[i+1]\),和上面一样，\(t_j\)要取\(a[i]\),那么第k+1到 i 只猫的等待时间为\(a[i]-a[k+1]+a[i]-a[k+2]\cdots +a[i]-a[i-1]+a[i]-a[i]\),将\(a[i]\)求一遍前缀和记为\(s[i]\),简化为\((i-k)*a[i]-s[i]+s[k]\)
状态转移方程为\(f[j][i]=f[j-1][k]+(i-k)*a[i]-s[i]+s[k],1\le j\le P,0\le k<i\)
-
斜率优化
将上式变形 \(f[j-1][k]+s[k]=k*a[i]-i*a[i]+s[i]+f[j][i]\)
可以把左边看成 y,右边k看成x，因此原式变成了\(y=k1*x+b\)的形式，因为斜率\(a[i]\)是单调递增的，所以原问题转化为求在(x,y)构成的点的集合中，求一条截距最小的直线，与任务安排2类似，可以用单调队列在\(O(m*p)\)的时间复杂度内完成。C++代码
#include<iostream> #include<cstring> #include<vector> #include<cmath> #include<algorithm> using namespace std; const int N=1e5+10,M=110; long long s1[N],a[N],s2[N],q[N],f[M][N]; long long get_y(int j,int k) { return f[j-1][k]+s2[k]; } int main() { int n,m,p; cin>>n>>m>>p; for(int i=2;i<=n;i++) { scanf("%lld",&s1[i]); s1[i]+=s1[i-1]; } for(int i=1;i<=m;i++) { int h,t; scanf("%d%d",&h,&t); a[i]=t-s1[h]; } sort(a+1,a+m+1); for(int i=1;i<=m;i++) s2[i]=s2[i-1]+a[i]; memset(f,0x3f,sizeof f); for(int i=0;i<=p;i++) f[i][0]=0; for(int j=1;j<=p;j++) { int hh=0,tt=0; q[hh]=0; for(int i=1;i<=m;i++) { while(hh<tt&&(get_y(j,q[hh+1])-get_y(j,q[hh]))<=a[i]*(q[hh+1]-q[hh])) hh++; int k=q[hh]; f[j][i]=f[j-1][k]+(i-k)*a[i]-s2[i]+s2[k]; while(hh<tt&&(get_y(j,q[tt])-get_y(j,q[tt-1]))*(i-q[tt])>=(get_y(j,i)-get_y(j,q[tt]))*(q[tt]-q[tt-1])) tt--; q[++tt]=i; } } printf("%lld",f[p][m]); }STL函数和C++语法
文件读入数据
数据样例 data.txt
| 12 14 45 78 100 18 7 45 |
|||||
|---|---|---|---|---|---|
一个个数字读取
#include <iostream>
#include <cstring>
#include<string>
#include<fstream>
#include<sstream>
using namespace std;
int main()
{
ifstream file1("data.txt");
string s;
char line[100];
while(file1.getline(line,sizeof line)){
stringstream s1(line);
int x;
while(s1>>x) cout<<x<<" ";
}
system("pause");
}
若文本数据中，有逗号分隔符，例如
12,14,45,78,100,
18,7,45
这样的，只需要再getline的第三个函数加上分隔符
#include <iostream>
#include <cstring>
#include<string>
#include<fstream>
#include<sstream>
using namespace std;
int main()
{
ifstream file1("data.txt");
char line[100];
while(file1.getline(line,sizeof line,',')){
stringstream s1(line);
int x;
while(s1>>x) cout<<x<<" ";
}
system("pause");
}
cin开流
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
multiset
multiset<int>q;
//定义一个multiset，尖括号里写类型
//如果是自定义类型，需要重载小于号
q.insert(x);
//插入一个数 x
q.clear();
//清空
q.erase(x);
//删除容器中的所有值为 x 的数
q.erase(it);
//删除容器中迭代器it指向的元素
q.empty();
//返回bool值，如果容器为空返回true，否则返回false
q.size()
//返回元素个数
q.begin();
//返回首个元素的迭代器
q.end();
//返回最后一个元素的下一个位置的迭代器
q.count(x);
//返回容器中 x 的个数
q.find(x);
//返回容器中第一个x的位置（迭代器），如果没有就返回q.end()
q.lower_bound(x);
//返回容器中第一个大于等于x的数的迭代器
q.upper_bound(x);
//返回容器中第一个大于x的数的迭代器
输出int128__
void print128(i128 x)//注意x不能为0
{
if (!x)
return;
print128(x / 10);
putchar(x % 10 + '0');
}
ostream &operator<<(ostream &os, const i128 &v) {//v=可以为0
if (v <= 1000000000000000000) {
return os << ll(v);
}
return os << ll(v / 1000000000000000000) << setw(18) << setfill('0') << ll(v % 1000000000000000000);
}
黑科技
自动取模类（jiangly)
using i64 = long long;
template<class T>
constexpr T power(T a, i64 b) {
T res = 1;
for (; b; b /= 2, a *= a) {
if (b % 2) {
res *= a;
}
}
return res;
}
constexpr i64 mul(i64 a, i64 b, i64 p) {
i64 res = a * b - i64(1.L * a * b / p) * p;
res %= p;
if (res < 0) {
res += p;
}
return res;
}
template<i64 P>
struct MLong {
i64 x;
constexpr MLong() : x{} {}
constexpr MLong(i64 x) : x{norm(x % getMod())} {}
static i64 Mod;
constexpr static i64 getMod() {
if (P > 0) {
return P;
} else {
return Mod;
}
}
constexpr static void setMod(i64 Mod_) {
Mod = Mod_;
}
constexpr i64 norm(i64 x) const {
if (x < 0) {
x += getMod();
}
if (x >= getMod()) {
x -= getMod();
}
return x;
}
constexpr i64 val() const {
return x;
}
explicit constexpr operator i64() const {
return x;
}
constexpr MLong operator-() const {
MLong res;
res.x = norm(getMod() - x);
return res;
}
constexpr MLong inv() const {
assert(x != 0);
return power(*this, getMod() - 2);
}
constexpr MLong &operator*=(MLong rhs) & {
x = mul(x, rhs.x, getMod());
return *this;
}
constexpr MLong &operator+=(MLong rhs) & {
x = norm(x + rhs.x);
return *this;
}
constexpr MLong &operator-=(MLong rhs) & {
x = norm(x - rhs.x);
return *this;
}
constexpr MLong &operator/=(MLong rhs) & {
return *this *= rhs.inv();
}
friend constexpr MLong operator*(MLong lhs, MLong rhs) {
MLong res = lhs;
res *= rhs;
return res;
}
friend constexpr MLong operator+(MLong lhs, MLong rhs) {
MLong res = lhs;
res += rhs;
return res;
}
friend constexpr MLong operator-(MLong lhs, MLong rhs) {
MLong res = lhs;
res -= rhs;
return res;
}
friend constexpr MLong operator/(MLong lhs, MLong rhs) {
MLong res = lhs;
res /= rhs;
return res;
}
friend constexpr std::istream &operator>>(std::istream &is, MLong &a) {
i64 v;
is >> v;
a = MLong(v);
return is;
}
friend constexpr std::ostream &operator<<(std::ostream &os, const MLong &a) {
return os << a.val();
}
friend constexpr bool operator==(MLong lhs, MLong rhs) {
return lhs.val() == rhs.val();
}
friend constexpr bool operator!=(MLong lhs, MLong rhs) {
return lhs.val() != rhs.val();
}
};
template<>
i64 MLong<0LL>::Mod = i64(1E18) + 9;
template<int P>
struct MInt {
int x;
constexpr MInt() : x{} {}
constexpr MInt(i64 x) : x{norm(x % getMod())} {}
static int Mod;
constexpr static int getMod() {
if (P > 0) {
return P;
} else {
return Mod;
}
}
constexpr static void setMod(int Mod_) {
Mod = Mod_;
}
constexpr int norm(int x) const {
if (x < 0) {
x += getMod();
}
if (x >= getMod()) {
x -= getMod();
}
return x;
}
constexpr int val() const {
return x;
}
explicit constexpr operator int() const {
return x;
}
constexpr MInt operator-() const {
MInt res;
res.x = norm(getMod() - x);
return res;
}
constexpr MInt inv() const {
assert(x != 0);
return power(*this, getMod() - 2);
}
constexpr MInt &operator*=(MInt rhs) & {
x = 1LL * x * rhs.x % getMod();
return *this;
}
constexpr MInt &operator+=(MInt rhs) & {
x = norm(x + rhs.x);
return *this;
}
constexpr MInt &operator-=(MInt rhs) & {
x = norm(x - rhs.x);
return *this;
}
constexpr MInt &operator/=(MInt rhs) & {
return *this *= rhs.inv();
}
friend constexpr MInt operator*(MInt lhs, MInt rhs) {
MInt res = lhs;
res *= rhs;
return res;
}
friend constexpr MInt operator+(MInt lhs, MInt rhs) {
MInt res = lhs;
res += rhs;
return res;
}
friend constexpr MInt operator-(MInt lhs, MInt rhs) {
MInt res = lhs;
res -= rhs;
return res;
}
friend constexpr MInt operator/(MInt lhs, MInt rhs) {
MInt res = lhs;
res /= rhs;
return res;
}
friend constexpr std::istream &operator>>(std::istream &is, MInt &a) {
i64 v;
is >> v;
a = MInt(v);
return is;
}
friend constexpr std::ostream &operator<<(std::ostream &os, const MInt &a) {
return os << a.val();
}
friend constexpr bool operator==(MInt lhs, MInt rhs) {
return lhs.val() == rhs.val();
}
friend constexpr bool operator!=(MInt lhs, MInt rhs) {
return lhs.val() != rhs.val();
}
};
template<>
int MInt<0>::Mod = 998244353;
template<int V, int P>
constexpr MInt<P> CInv = MInt<P>(V).inv();
constexpr int P = 1e9+7;
using mint = MInt<P>;