SP26346 NINJA3 - STUNNING GCD
思路
首先观察到数据范围很大,所以暴力模拟是不可行的,所以我们思考其他的性质。
显而易见地,\(X\) 和 \(Y\) 一定都是 \(N\) 的倍数,所以最大公因数一定都是 \(N\) 的倍数。
那么我们可以先将 \(X\) 和 \(Y\) 除以一个 \(N\),那么剩下的就是 \(10 \ldots 010 \ldots 01\ldots\),中间一段 \(0\) 的个数为 \(N\) 的位数 \(-1\)。
对于形如 \(10 \ldots 010 \ldots 01\ldots\) 的数,我们称它的 \(1\) 的个数为段数 \(n\)。那么我们可以发现只有当某个数的段数为 \(k\times n,k\in N^+\) 时,才是段数为 \(n\) 的数的倍数。
证明很好证,我们可以用反证法,首先假设一个数的段数为 \(A\),另一个数的段数为 \(A\),而 \(A\) 不是 \(B\) 的倍数,我们可以随意举一个例子,如下图。
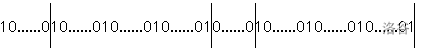
第二个数可以如上图一样将第一个数分为若干份,因为 \(A\) 不是 \(B\) 的倍数,所以一定会留下若干个 \(1\) 不能被分掉,所以第一个数也不是第二个数的倍数。
得到上面的结论后,我们可以发现中间的 \(0\) 没有用,所以我们可以只关注 \(1\) 的数量,而 \(1\) 的数量就是题目中给的重复几次的次数 \(a\) 和 \(b\)。
那么段数为 \(\gcd(a,b)\) 的数一定是 \(X\) 和 \(Y\) 除以 \(N\) 后的最大公因数。
所以正确答案就很显然了。
我们只需要输出 \(\gcd(a,b)\) 遍的 \(N\) 即可。
AC 代码
#include<iostream>
#include<cstdio>
using namespace std;
long long T,n,a,b;
long long gcd(long long a,long long b){return (!b)?a:gcd(b,a%b);}
int main()
{
scanf("%lld",&T);
while(T--)
{
scanf("%lld%lld%lld",&n,&a,&b);
for(long long i=1;i<=gcd(a,b);++i) printf("%lld",n);
puts("");
}
}